Tìm tất cả các giá trị của tham số thực m để phương trình sau có đúng 3 nghiệm thực phân biệt 9^x^2
Câu hỏi
Nhận biếtTìm tất cả các giá trị của tham số thực \(m\) để phương trình sau có đúng \(3\) nghiệm thực phân biệt \({9^{{x^2}}} - {2.3^{{x^2} + 1}} + 3m - 1 = 0\).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Cách 1: Ẩn phụ rồi vẽ BBT:
\(\begin{array}{l}\,\,\,\,\,\,\,{9^{{x^2}}} - {2.3^{{x^2} + 1}} + 3m - 1 = 0\\ \Leftrightarrow {\left( {{3^{{x^2}}}} \right)^2} - {2.3.3^{{x^2}}} + 3m - 1 = 0\end{array}\)
Đặt \({3^{{x^2}}} = t > 1\), khi đó phương trình trở thành: \({t^2} - 6t + 3m - 1 = 0\)\( \Leftrightarrow m = \dfrac{{{t^2} - 6t - 1}}{{ - 3}} = f\left( t \right)\,\,\,\left( 1 \right)\).
Ta có: \(f'\left( t \right) = \dfrac{{2t - 6}}{{ - 3}} = 0 \Rightarrow t = 3\).
BBT:
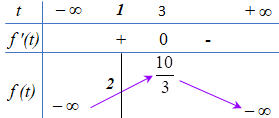
Để phương trình ban đầu có 3 nghiệm phân biệt thì phương trình (1) phải có 1 nghiệm \(t = 1\) và 1 nghiệm \(t > 1\).
Vậy \(m = 2\).
Cách 2: Cô lập \(m\)rồi vẽ luôn BBT
\({9^{{x^2}}} - {2.3^{{x^2} + 1}} + 3m - 1 = 0\)\( \Leftrightarrow 3m = 1 + {2.3^{{x^2} + 1}} - {9^{{x^2}}}\)
+ Vẽ BBT của hàm số \(f\left( x \right) = 1 + {2.3^{{X^2} + 1}} - {9^{{X^2}}}\).
+ Vào chức năng Mode + 7, nhập\(\left\{ \begin{array}{l}f\left( x \right) = 1 + {2.3^{{X^2} + 1}} - {9^{{X^2}}}\\St{\rm{ar}}t = - 5\\En{\rm{d}} = 5\\Step = \dfrac{1}{{19}}\end{array} \right.\), thu được:
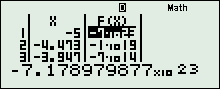
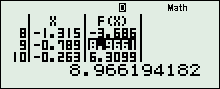
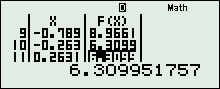
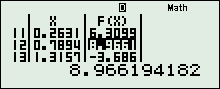
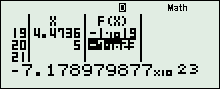
+ Quan sát ta thấy: \(f\left( x \right)\) chạy từ \( - \infty \) tăng lên 9, rồi giảm xuống 6, rồi lại tăng lên 9 và giảm xuống \( - \infty \), Vậy BBT là:
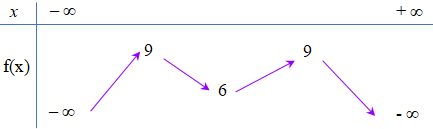
Vậy để phương trình có 3 nghiệm \( \Rightarrow 3m = 6 \Leftrightarrow m = 2\).
Chọn C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
