Ông A dự định sử dụng hết 6,5m^3 kính để làm một bể cá bằng kính có dạ
Câu hỏi
Nhận biếtÔng \(A \) dự định sử dụng hết \(6,5{m^3} \) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
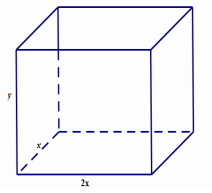
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y\,\,\left( {x,y > 0} \right)\).
Diện tích phần lắp kính là:
\(\begin{array}{l}2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\\ \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}} = \frac{{\sqrt {13} }}{2}.\end{array}\)
Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\)
Ta có: \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt {39} }}{6}\\x = - \frac{{\sqrt {39} }}{6}\left( L \right)\end{array} \right.\)
Bảng biến thiên:
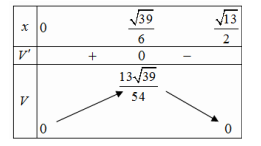
Vậy \({V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,50\,{m^3}\)
Chọn D.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.