Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình
Câu hỏi
Nhận biếtNgười ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình tròn là \(20\) mét và \(15\) mét. Khoảng cách giữa hai tâm của hai hình tròn là \(30\) mét. Chi phí làm mỗi mét vuông phần giao của hai hình tròn là \(300\) nghìn đồng và chi phí làm mỗi mét vuông phần còn lại là \(100\) nghìn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào nhất trong các số dưới đây?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
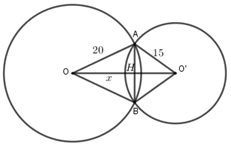
Đặt \(OH = x \Rightarrow O'H = 30 - x\).
Ta có: \(\Delta AHO\) vuông tại \(H\) nên \(A{H^2} = O{A^2} - O{H^2} = 400 - {x^2}\)
\(\Delta AHO'\) vuông tại \(H\) nên : \(A{H^2} = O'{A^2} - O'{H^2} = 225 - {\left( {30 - x} \right)^2}\)
\( \Rightarrow 400 - {x^2} = 225 - {\left( {30 - x} \right)^2} \Leftrightarrow x = \frac{{215}}{{12}}\)
\( \Rightarrow OH = \frac{{215}}{{12}},\,\,\,O'H = \frac{{145}}{{12}}.\)
Khi đó \(AH = \sqrt {O{A^2} - O{H^2}} = \frac{{5\sqrt {455} }}{{12}}\).
Ta tính diện tích phần giao của hai đường tròn (bằng tổng diện tích hai hình viên phân chắn bởi cung \(AB\) và dây \(AB\) ở mỗi đường tròn)
+) Xét hình viên phân tạo bởi dây và cung \(AB\) của hình tròn tâm \(O\) bán kính \(20\).
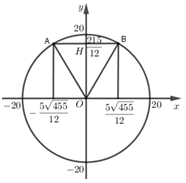
Chọn hệ trục tọa độ như hình vẽ trên.
Ở đó hình viên phân tạo bởi cung và dây \(AB\) giới hạn bởi nửa đường tròn \(y = \sqrt {400 - {x^2}} \) và đường thẳng \(y = \frac{{215}}{{12}}\)
Phương trình hoành độ giao điểm \(\sqrt {400 - {x^2}} = \frac{{215}}{{12}} \Leftrightarrow x = \pm \frac{{5\sqrt {455} }}{{12}}\).
Do đó diện tích \({S_1} = \int\limits_{ - \frac{{5\sqrt {455} }}{{12}}}^{\frac{{5\sqrt {455} }}{{12}}} {\left( {\sqrt {400 - {x^2}} - \frac{{215}}{{12}}} \right)dx} \approx 24,96\left( m \right)\).
+) Xét hình viên phân tạo bởi dây và cung \(AB\) của hình tròn tâm \(O'\) bán kính \(15\).
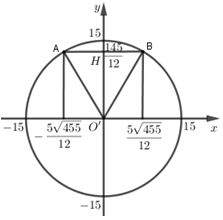
Chọn hệ trục tọa độ như hình vẽ trên. Ở đó hình viên phân tạo bởi cung và dây \(AB\) giới hạn bởi nửa đường tròn \(y = \sqrt {225 - {x^2}} \) và đường thẳng \(y = \frac{{145}}{{12}}\) .
Phương trình hoành độ giao điểm \(\sqrt {225 - {x^2}} = \frac{{145}}{{12}} \Leftrightarrow x = \pm \frac{{5\sqrt {455} }}{{12}}\).
Do đó diện tích \({S_2} = \int\limits_{ - \frac{{5\sqrt {455} }}{{12}}}^{\frac{{5\sqrt {455} }}{{12}}} {\left( {\sqrt {225 - {x^2}} - \frac{{145}}{{12}}} \right)dx} \approx 35,3\left( m \right)\).
Diện tích phần giao của hai hình tròn là: \(S = {S_1} + {S_2} = 24,96 + 35,3 = 60,26\left( m \right)\).
Diện tích phần còn lại của hình tròn là: \(S' = \left( {\pi {{.20}^2} - 60,26} \right) + \left( {\pi {{.15}^2} - 60,26} \right) \approx 1842,98\left( m \right)\).
Vậy tổng chi phí là: \(1842,98 \times 100.000 + 60,26 \times 300.000 = 202.376.000\).
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.