Người ta sử dụng 5 cuốn sách tiếng Anh, 6 cuốn tiếng Pháp, 7
Câu hỏi
Nhận biếtNgười ta sử dụng 5 cuốn sách tiếng Anh, 6 cuốn tiếng Pháp, 7 cuốn tiếng Nhật (các cuốn sách cùng loại giống nhau) để làm giải thưởng cho 9 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 9 học sinh trên chó hai bạn Lan và Nam. Tìm sác xuất để hai bạn Lan và Nam có giải thưởng giống nhau.
Đáp án đúng: C
Lời giải của Tự Học 365
Lời giải chi tiết:
Gọi A là biến cố "Lan, Nam có phần thưởng giống nhau".
Có 2 phần (tiếng Anh, tiếng Pháp), 3 phần (tiếng Anh, tiếng Nhật) và 4 phần (tiếng Pháp, tiếng Nhật). Ta có: n(Ω) =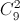 
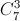= 1260
Trường hợp 1: Lan, Nam nhận sách (tiếng Anh, tiếng Pháp), số khả năng: 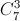= 35
Trường hợp 2:Lan, Nam nhận sách (tiếng Anh, tiếng Nhật), số khả năng: 
= 105
Trường hợp 1: Lan, Nam nhận sách (tiếng Pháp, tiếng Nhật),số khả năng: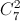 
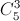= 210
Suy ra n ( A ) = 35 + 105 + 210 = 350 ⇒ p(A) =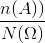 
= 
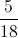
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
