Một thầy giáo có 12 quyển sách đôi một khác nhau trong đó có 5 quyển s
Câu hỏi
Nhận biếtMột thầy giáo có 12 quyển sách đôi một khác nhau trong đó có 5 quyển sách Toán, 4 quyển sách Vật lý, và 3 quyển sách Hóa học. Ông muốn lấy ra 6 quyển đem tặng cho 6 học sinh A, B, C, D, E, F mỗi em một quyển.Tính xác suất để sau khi tặng sách xong mỗi một trong ba loại Toán, Vật lý, Hóa học đều còn lại ít nhất một quyển.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta thấy không thể chọn sao cho cùng hết 2 loại sách
Số cách chọn 6 quyển sách từ 12 sách là |Ω| =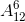 
= 665280.
Gọi A là biến cố: “Sau khi tặng sách xong mỗi một trong ba loại Toán, Vật lý, Hóa học đều còn lại ít nhất một quyển.”
P(A) = 1 - P(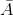
)
Số cách chọn sao cho không còn sách Toán: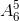
.7 = 5040
Số cách chọn sao cho không còn sách Vật lý: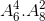
= 20160
Số cách chọn sao cho không còn sách Hóa học: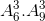 
= 60480
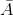
() = 5040 + 20160 + 60480 = 85680
P () = 
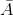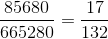
Vậy xác xuất cần tìm làP () = 1 -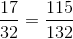 
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
