Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện càng nhanh càng
Câu hỏi
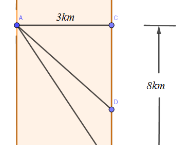
Nhận biếtMột người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể chèo thuyền trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B. Biết anh ấy có thể chèo thuyển 6km/h, chạy 8km/h và quãng đường BC = 8km. Biết tốc độ dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
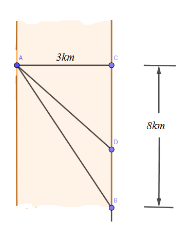
Gọi độ dài đoạn CD là x (km, \(0 \le x \le 8\)).
Quãng đường AD dài là: \(\sqrt {A{C^2} + D{C^2}} = \sqrt {{3^2} + {x^2}} = \sqrt {9 + {x^2}} \)(km)
Quãng đường BD dài là: 8 – x (km)
Thời gian người đó đi đến B: \(\dfrac{{\sqrt {9 + {x^2}} }}{6} + \dfrac{{8 - x}}{8}\) (h)
Xét hàm số \(y = \dfrac{{\sqrt {9 + {x^2}} }}{6} + \dfrac{{8 - x}}{8},\,x \in \left[ {0;8} \right]\)
\(y' = \dfrac{x}{{6\sqrt {9 + {x^2}} }} - \dfrac{1}{8}\)
\(y' = 0 \Leftrightarrow \dfrac{x}{{6\sqrt {9 + {x^2}} }} - \dfrac{1}{8} = 0 \Leftrightarrow 4x = 3\sqrt {9 + {x^2}} \Leftrightarrow \left\{ \begin{array}{l}
16{x^2} = 9(9 + {x^2})\\
x \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x^2} = \dfrac{{81}}{7}\\
x \ge 0
\end{array} \right. \Leftrightarrow x = \dfrac{9}{{\sqrt 7 }}\)
Bảng biến thiên:
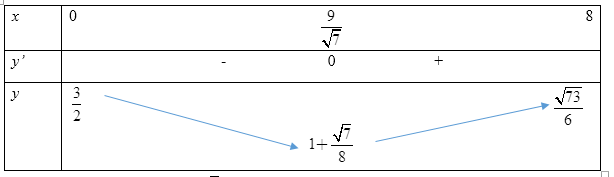
Vậy, thời gian đi đến B ngắn nhất là \(1 + \dfrac{{\sqrt 7 }}{8}\) (h).
Chọn: B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.