Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biểnAB=5km. Trên bờ biển có một cái kho ở v
Câu hỏi
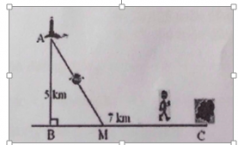
Nhận biếtMột ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển\(AB=5km\). Trên bờ biển có một cái kho ở vị trí C cách B một khoảng \(7km\). Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc \(4km/h\) rồi đi bộ đến C với vận tốc \(6km/h\). Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi độ dài đoạn MB là \(x,\,\,(0\le x\le 7,km)\) \(\Rightarrow MC=7-x\)
Tam giác ABM vuông tại B \(\Rightarrow AM=\sqrt{B{{M}^{2}}+A{{B}^{2}}}=\sqrt{{{x}^{2}}+{{5}^{2}}}=\sqrt{{{x}^{2}}+25}\)
Thời gian người đó đi từ A tới C: \(\frac{\sqrt{{{x}^{2}}+25}}{4}+\frac{7-x}{6}\)
Xét hàm số \(f(x)=\frac{\sqrt{{{x}^{2}}+25}}{4}+\frac{7-x}{6},\,\,x\in \left[ 0;7 \right]\)
\(y'=\frac{x}{4\sqrt{{{x}^{2}}+25}}-\frac{1}{6}\)\(y'=0\Leftrightarrow \frac{x}{4\sqrt{{{x}^{2}}+25}}-\frac{1}{6}=0\Leftrightarrow \frac{x}{4\sqrt{{{x}^{2}}+25}}=\frac{1}{6}\Leftrightarrow 3x=2\sqrt{{{x}^{2}}+25}\Leftrightarrow 9{{x}^{2}}=4{{x}^{2}}+100\Leftrightarrow {{x}^{2}}=20\Rightarrow x=2\sqrt{5}\)
Bảng biến thiên:
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là \(2\sqrt{5}\).
Chọn: A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
