Một màn ảnh hình chữ nhật cao 14m được đặt ở độ cao 18m so với tầm mắt (tính đầu mép dưới của màn hì
Câu hỏi
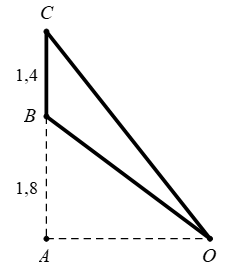
Nhận biếtMột màn ảnh hình chữ nhật cao \(1,4m\) được đặt ở độ cao \(1,8m\) so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Lời giải:
Với bài toán này, ta cần xác định \(OA\) để góc \(\widehat{BOC}\) lớn nhất. Điều này xảy ra \(\Leftrightarrow \)\(\tan \widehat{BOC}\) lớn nhất.
Đặt \(OA=x\,\,\,\left( m \right)\) với \(x>0.\) Ta có:
\(\tan \widehat{BOC}=\tan \left( \widehat{AOC}-\widehat{AOB} \right)=\frac{\tan \widehat{AOC}-\tan \widehat{AOB}}{1+\tan \widehat{AOC}.tan\widehat{AOB}}\)\(=\frac{\frac{AC}{OA}-\frac{AB}{OA}}{1+\frac{AC.AB}{O{{A}^{2}}}}=\frac{\frac{1,4}{x}}{1+\frac{3,2.1,8}{{{x}^{2}}}}=\frac{1,4x}{{{x}^{2}}+5,76}.\)
Xét hàm số \(f\left( x \right)=\frac{1,4x}{{{x}^{2}}+5,76}\) trên \(\left( 0;+\,\infty \right),\) có:
\({f}'\left( x \right)=\frac{-\,1,4{{x}^{2}}+1,4.5,76}{{{\left( {{x}^{2}}+5,76 \right)}^{2}}};\,\,{f}'\left( x \right)=0\Leftrightarrow \left\{ \begin{align} & x>0 \\ & {{x}^{2}}=5,76 \\\end{align} \right.\Leftrightarrow x=2,4.\)
Tính các giá trị \(f\left( 0 \right)=0;\,\,f\left( 2,4 \right)=\frac{7}{24};\,\,\underset{x\,\to \,+\,\infty }{\mathop{\lim }}\,f\left( x \right)=0\) suy ra \(\underset{\left( 0;+\,\infty \right)}{\mathop{\max }}\,f\left( x \right)=\frac{7}{24}.\)
Vậy khoảng cách \(OA\) cần tìm là \(2,4\,\,m.\)
Chọn A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.