Một đường dây điện được nối từ một nhà máy điện ở A đến điểm C trên một hòn đảo. Khoảng cách từ C đế
Câu hỏi
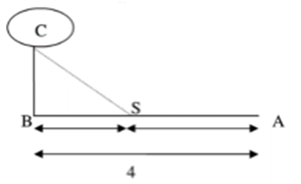
Nhận biếtMột đường dây điện được nối từ một nhà máy điện ở A đến điểm C trên một hòn đảo. Khoảng cách từ C đến B là 1 \(km.\) Khoảng cách từ B đến A là 4 \(km.\) Mỗi \(km\) dây điện đặt dưới nước chi phí là 100 triệu đồng, còn đặt dưới đất là 80 triệu đồng. Người ta mắc dây diện từ A qua điểm S trên bờ cách A một khoảng \(x\) rồi đến C. Chọn giá trị của \(x\) để chi phí tốn ít nhất trong các phương án sau.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Đặt SA = x (km) \(\left( 0 Độ dài đoạn thẳng \(SB\) là \(SB=AB-SA=4-x\,\,km.\) Độ dài đoạn thẳng \(SC\) là \(SC=\sqrt{B{{C}^{2}}+S{{B}^{2}}}=\sqrt{{{1}^{2}}+{{\left( 4-x \right)}^{2}}}=\sqrt{{{x}^{2}}-8x+17}\,\,km.\) Do đó, chi phí để mắc dây diện từ \(C\,\,\xrightarrow{{}}\,\,A\) là \(T=\)\(100\sqrt{{{x}^{2}}-8x+17}+80x\) triệu đồng. Xét hàm số \(f\left( x \right)=10\sqrt{{{x}^{2}}-8x+17}+8x\) trên khoảng \(\left( 0;4 \right),\) có \(\begin{array}{l} Dựa vào bảng biến thiên, ta thấy \(\min f\left( x \right)=f\left( \frac{8}{3} \right).\) Vậy giá trị cần tìm là \(x=\frac{8}{3}\,\,km.\) Chọn C
f'\left( x \right) = 100.\frac{{2x - 8}}{{2\sqrt {{x^2} - 8x + 17} }} + 80 = \frac{{100\left( {x - 4} \right)}}{{\sqrt {{x^2} - 8x + 17} }} + 80\\
f'\left( x \right) = 0 \Leftrightarrow 100\left( {x - 4} \right) + 80\sqrt {{x^2} - 8x + 17} = 0\\
\Leftrightarrow 4\sqrt {{x^2} - 8x + 17} = 5\left( {4 - x} \right)\\
\Leftrightarrow 16\left( {{x^2} - 8x + 17} \right) = 25{x^2} - 200x + 400\\
\Leftrightarrow 9{x^2} - 72x + 128 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{8}{3}\,\,\,\left( {tm} \right)\\
x = \frac{{16}}{3}\,\,\,\left( {ktm} \right)
\end{array} \right.
\end{array}\)
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.