Lúc 10 giờ sáng trên sa mạc một nhà địa chất đang ở tại vị trí A anh ta muốn đến vị trí B (bằng ô tô
Câu hỏi
Nhận biếtLúc 10 giờ sáng trên sa mạc, một nhà địa chất đang ở tại vị trí \(A\), anh ta muốn đến vị trí \(B\) (bằng ô tô) trước 12 giờ trưa, với \(AB = 70\,km.\) Nhưng trong sa mạc thì xe chỉ có thể di chuyển với vận tốc là \(30\,km/h\). Cách vị trí \(A\) \(10\,km\) có một con đường nhựa chạy song song với đường thẳng nối từ\(A\) đến \(B\). Trên đường nhựa thì xe có thể di chuyển với vận tốc \(50\,km/h\). Tìm thời gian ít nhất để nhà địa chất đến vị trí \(B\)?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
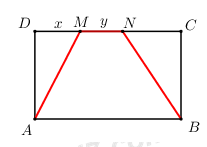
Giả sử ô tô đi theo đường gấp khúc \(AMNB\) như hình vẽ bên.
Đặt \(DM = x,\,\,MN = y \Rightarrow NC = 70 - x - y\).
\( \Rightarrow AM = \sqrt {D{M^2} + A{D^2}} = \sqrt {{x^2} + {{10}^2}} ,\,\,BN = \sqrt {B{C^2} + C{N^2}} = \sqrt {{{10}^2} + {{\left( {70 - x - y} \right)}^2}} \)
Thời gian ô tô đi hết quãng đường \(AM:\,\,{t_1} = \dfrac{{\sqrt {{x^2} + {{10}^2}} }}{{30}}\)
Thời gian ô tô đi hết quãng đường \(MN:\,\,{t_2} = \dfrac{y}{{50}}\)
Thời gian ô tô đi hết quãng đường \(NC:\,\,{t_3} = \dfrac{{\sqrt {{{10}^2} + {{\left( {70 - x - y} \right)}^2}} }}{{30}}\)
Khi đó tổng thời gian ô tô đi từ A đến B là:
\(t = {t_1} + {t_2} + {t_3} = \dfrac{{\sqrt {{x^2} + {{10}^2}} + \sqrt {{{\left( {70 - x - y} \right)}^2} + {{10}^2}} }}{{30}} + \dfrac{y}{{50}} \ge \dfrac{{\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} }}{{30}} + \dfrac{y}{{50}}\)
Xét hàm số \(f\left( y \right) = \dfrac{{\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} }}{{30}} + \dfrac{y}{{50}}\,\,\left( {0 < y < 70} \right)\) ta có:
\(\begin{array}{l}f'\left( y \right) = \dfrac{{y - 70}}{{30\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} }} + \dfrac{1}{{50}} = 0 \Leftrightarrow \dfrac{{5\left( {y - 70} \right) + 3\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} }}{{150\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} }} = 0\\ \Leftrightarrow 3\sqrt {{{\left( {70 - y} \right)}^2} + {{20}^2}} = 5\left( {70 - y} \right) \Leftrightarrow 9{\left( {70 - y} \right)^2} + {9.20^2} = 25{\left( {70 - y} \right)^2}\\ \Leftrightarrow 16{\left( {70 - y} \right)^2} = 3600 \Leftrightarrow {\left( {70 - y} \right)^2} = 225 \Leftrightarrow 70 - y = 15 \Leftrightarrow y = 55\end{array}\)
BBT:
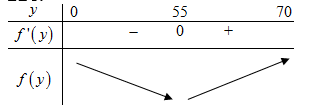
Dựa vào BBT \( \Rightarrow \min f\left( y \right) = f\left( {55} \right) = \dfrac{{29}}{{15}}\)
Vậy thời gian ít nhất để nhà địa chất đến vị trí B là \(\dfrac{{29}}{{15}}\) giờ = 1 giờ 56 phút.
Chọn C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.