Lăng trụ đều ABC.A’B’C’ AB = AA’ = a. M N là trung điểm AC BB’. Tính sin góc ( MN;( BA'C' ) )?
Câu hỏi
Nhận biếtLăng trụ đều ABC.A’B’C’, AB = AA’ = a. M, N là trung điểm AC, BB’. Tính \(\sin \widehat {\left( {MN;\left( {BA'C'} \right)} \right)}\)?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
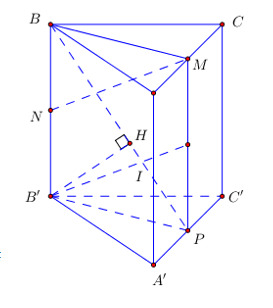
* Vẽ P, Q là trung điểm A’C’, MP.
* Tứ giác MNB’Q là hình bình hành \( \Rightarrow MN//B'Q\)
\( \Rightarrow \widehat {\left( {MN;\left( {BA'C'} \right)} \right)} = \widehat {\left( {B'Q;\left( {BA'C'} \right)} \right)}\)
* Nối \(B'Q \cap BP = I \Rightarrow B'Q \cap \left( {BA'C'} \right) = I\)
* Vẽ \(B'H \bot BP \Rightarrow B'H \bot \left( {BA'C'} \right)\)
\( \Rightarrow \widehat {\left( {B'I;\left( {BA'C'} \right)} \right)} = \widehat {\left( {B'I;IH} \right)} = \widehat {B'IH}\)
* Tam giác vuông B’PQ: \(B'Q = \sqrt {B'{P^2} + P{Q^2}} = \sqrt {\frac{{3{a^2}}}{4} + \frac{{{a^2}}}{4}} = a\)
* \(\Delta B'PM\) có I là trọng tâm \( \Rightarrow B'I = \frac{2}{3}a\)
* Tam giác vuông BB’P: \(\frac{1}{{B'{H^2}}} = \frac{1}{{{a^2}}} + \frac{4}{{3{a^2}}} = \frac{7}{{3{a^2}}} \Rightarrow B'H = \frac{{a\sqrt 3 }}{{\sqrt 7 }}\) * Tam giác vuông B’HI: \(\sin \widehat {B'IH} = \frac{{B'H}}{{B'I}} = \frac{{a\sqrt 3 }}{{\sqrt 7 }}:\frac{{2a}}{3} = \frac{{3\sqrt 3 }}{{2\sqrt 7 }} = \sqrt {\frac{{27}}{{28}}} \)
Chọn đáp án A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
