ID:41059)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh 4a và ![]()
Câu hỏi
Nhận biếtID:41059)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh 4a và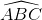 
= 600. Hình chiếu của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của OA. Góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 600. Tính thể tích của khối chóp S.ABCD theo a và cosin của góc tạo bởi đường thẳng AO và mặt phẳng (SCD).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
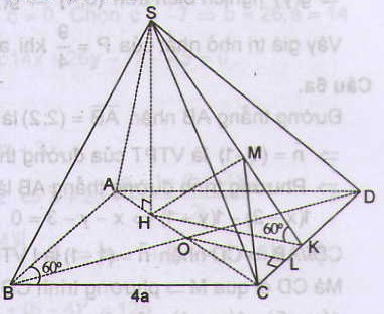
Ta có: SABCD = 2SABC = 4a.4a.sin600 = 8a2√3. Từ giả thiết AH = HO =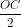 
Trong (ABCD), gọi L là chân đường cao hạ từ O của ∆OCD.
Kẻ KH //OL (K ∈ CD) => HK ⊥ CD (1)
Mà H là hình chiếu của S trên (ABCD) => SH ⊥ CD (2)
Từ (1), (2) => CD ⊥ (SHK)
Do góc giữa (SCD) và (ABCD) là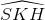 
= 600.
Tam giác OCD vuông tại O có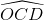 
= 600. => OL = OC. sin600 = a√3
∆HCK có OL // HK =>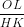 
= 
= 
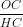=> HK =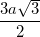 
∆ SHK vuông tại H => SH = HK. tan600 = 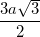.√3 =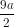 
.
Vậy VS.ABCD = 
.SH.SABCD = ..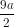 8√3a2 = 12√3a3
*Tính góc giữa AO và (SCD).
Nhận thấy góc giữa AO và (SCD) cũng chính là góc giữa HC và (SCD).
Trong (SHK) kẻ HM ⊥ KS (M ∈ SG) => HM ⊥ (SCD) (do CD ⊥ (SHK))
=> M là hình chiếu của H trên (SCD). Mà AO ∩ (SCD) = C
=> MC là hình chiếu của AO trên (SCD).
=> Góc giữa AO và (CSD) là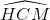 
Tam giác HKM vuông tại M => HM = HK. sin600 =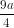 
Tam giác HCM vuông tại M => sin =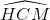 
= 
= 
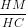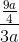=> cos =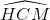 
.
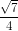Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.