Diện tích lớn nhất Smax của một hình chữ nhật nội tiếp trong nửa đường
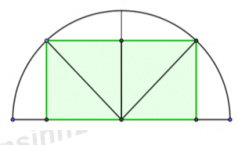
Câu hỏi
Nhận biếtDiện tích lớn nhất \({{S}_{\max }}\)của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(R=6cm\)nếu một cạnh của hình chữ nhật nằm dọc đường kính của hình tròn mà hình chữ nhật đó nội tiếp.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
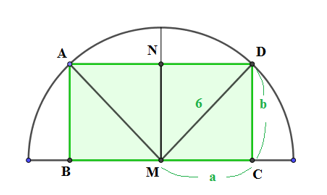
\({{S}_{ABCD}}=2{{S}_{CDNM}}=2.ab\overset{Cauchy}{\mathop{\le }}\,{{a}^{2}}+{{b}^{2}}={{6}^{2}}\Rightarrow {{S}_{\max }}=36\,(c{{m}^{2}})\) khi và chỉ khi \(a=b=3\sqrt{2}\,(cm)\).
Chọn: B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.