Có bao nhiêu số tự nhiên có 6 chữ số khác nhau mà trong mỗi số luôn lu
Câu hỏi
Nhận biếtCó bao nhiêu số tự nhiên có 6 chữ số khác nhau mà trong mỗi số luôn luôn có mặt ba chữ số chẵn và ba chữ số lẻ, các chữ số chẵn không đứng cạnh nhau.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Giả sử số có 6 chữ số khác nhau có dạng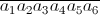 
( a ≠ 0; ai ≠ aj ⇔ i ≠ j)
Vì các chữ số chẵn không được đứng cạnh nhau do vậy ta sắp xếp vị trí các chữ số chẵn trước.
TH1: a1 nhận giá trị chẵn thì vị trí 2 chữ số chẵn còn lại là (a3 ; a5); (a3 ; a6); (a6 ; a4). Do vậy có 3 cách chọn vị trí cho các chữ số chẵn
Giả sử (a1 ; a3 ; a5), khi đó có 4 cách chọn giá trị cho (a1 ∈ {2; 4; 6; 8}) và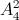 
cách chọn giá trị cho a3; a5; 
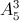cách chọn giá trị cho a2; a4; a6. Theo quy tắc nhân có: 3. 4. 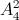. 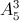= 8640 số
TH2: a2 nhận giá trị chẵn thì vị trí 2 chữ số chẵn còn lại là (a6 ; a4). Do vậy có 1 cách chọn vị trí cho các chữ số chẵn . Khi đó có 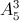cách chọn giá trị cho a2 ; a4 ; a6, cách chọn giá trị cho a1 ; a3 ; a5 theo quy tắc nhân ta có 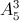. 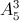= 3600 số. Vậy có 3600 + 8640 = 12240 số cần tìm.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.