Có 10 viên bi đỏ có bán kính khác nhau, 5 viên bi xanh có bá
Câu hỏi
Nhận biếtCó 10 viên bi đỏ có bán kính khác nhau, 5 viên bi xanh có bán kính khác nhau và 3 viên bi vàng có bán kính khác nhau . Hỏi có bao nhiêu cách chọn ra 9 viên bi có đủ ba màu?
Đáp án đúng: D
Lời giải của Tự Học 365
Lời giải chi tiết:
Số cách chọn 9 viên bi tùy ý là :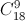 
Những trường hợp không đủ ba viên bi khác nhau là :
+Không có bi đỏ: Khả năng này không xảy ra vì tổng các viên bi xanh và vàng chỉ là 8
+Không có bi xanh: có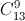 
cách
+Không có bi vàng : có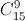 
cách
Mặt khác trong các cách chọn không có bi xanh , không có bi vàng thì có cách chọn 9 viên bi đỏ được tính hai lần.
Vậy số cách chọn 9 viên bi có đủ cả ba màu là :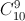 
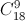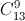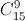+ - - = 42910 cách.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
