Cho tứ diện ABCD có AB = AC = a√2, BD = CD = a √3, BC = 2a, góc tạo bở
Câu hỏi
Nhận biếtCho tứ diện ABCD có AB = AC = a√2, BD = CD = a √3, BC = 2a, góc tạo bởi hai mặt phẳng (ABC) và (BCD) bằng 450. Tính theo a thể tích khối tứ diện ABCD và khoảng cách từ B đến mặt phẳng (ACD).
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Gọi M là trung điêm BC
từ các tam giác cân ABC, DBC
=> AM ⊥ BC, DM ⊥ BC
từ giả thiết =>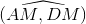 
= 450 => 
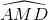= 450 hoặc 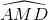= 1350
TH1: 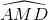= 450
Sử dụng định lý Pytago trong tam giác vuông ABM và BDM => AM = a, DM = a√2
Kẻ AH⊥MD tại H. vì BC⊥(ADM) => BC⊥AH=> AH⊥(BCD). Khi đó:
AH = AM sin450 =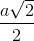 
; SBCD = DM.BC.1/2 = a2√2
Suy ra VABCD = 
AH.SBCD =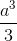 
Sử dụng định lý cô sin cho ∆AMD => AD = a => AC2 + AD2 = 3a2 = CD2 => ∆ACD vuông tại A
Suy ra SACD = 
AC.AD =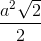 
=> d(B,(ACD)) = 
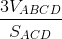= a√2
TH2.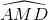 = 1350
Tương tự ta có VABCD = 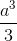; d(B,(ACD)) = 
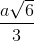(AD = a√5)
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.