Cho tấm bìa hình vuông cạnh 50 cm. Để làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ 4 tam giác
Câu hỏi
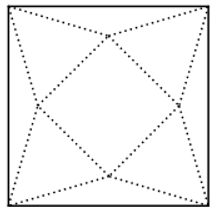
Nhận biếtCho tấm bìa hình vuông cạnh 50 cm. Để làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ 4 tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên, ghép lại thành môt hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình bằng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi cạnh đáy của mô hình kim tự tháp bằng x \(\Rightarrow HE=x\)
Gọi O là tâm hình vuông ABCD \(\Rightarrow O\) cũng là tâm hình vuông EFGH.
Xét tam giác OHE vuông cân tại O nên \(OH=OE=\frac{x}{\sqrt{2}}\Leftrightarrow PE=OP-OE=25-\frac{x}{\sqrt{2}}\)
Xét tam giác vuông AOE có: \(AE=\sqrt{A{{P}^{2}}+P{{E}^{2}}}=\sqrt{625+{{\left( 25-\frac{x}{\sqrt{2}} \right)}^{2}}}\)
Giả sử sau khi gấp lên ta được hình chóp S.EFGH như sau:
(Với \(S\equiv A\equiv B\equiv C\equiv D\))
Ta có \(SO=\sqrt{S{{E}^{2}}-O{{E}^{2}}}=\sqrt{A{{E}^{2}}-O{{E}^{2}}}=\sqrt{625+{{\left( 25-\frac{x}{\sqrt{2}} \right)}^{2}}-\frac{{{x}^{2}}}{2}}\)
Khi đó \({{V}_{S.EFGH}}=\frac{1}{3}SO.{{S}_{EFGH}}=\frac{1}{3}\sqrt{625+{{\left( 25-\frac{x}{\sqrt{2}} \right)}^{2}}-\frac{{{x}^{2}}}{2}}.{{x}^{2}}\)
Đến đây thử từng đáp án ta thấy khi \(x=20\sqrt{2}\) thì V đạt GTLN.
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
