Cho một tứ diện đều S.ABC có chiều cao h. Ở ba góc của tứ diện, người
Câu hỏi
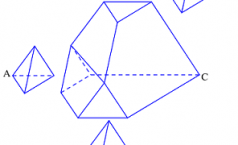
Nhận biếtCho một tứ diện đều \(S.ABC\) có chiều cao h. Ở ba góc của tứ diện, người ta cắt đi các tứ diện đều có chiều cao x để khối đa diện còn lại có thể tích bằng một nửa thể tích khối tứ diện đều ban đầu. Tìm x.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
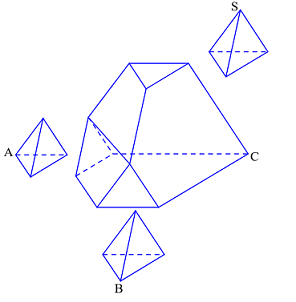
Tứ diện đều .. có chiều cao h \( \Rightarrow \) Độ dài cạnh của tứ diện \(S.ABC\) là: \(\dfrac{{3h}}{{\sqrt 6 }} = \dfrac{{h\sqrt 6 }}{2}\)
\( \Rightarrow \) Thể tích của khối tứ diện \(S.ABC\) là: \({V_{S.ABC}} = \dfrac{{{{\left( {\dfrac{{h\sqrt 6 }}{2}} \right)}^3}\sqrt 2 }}{{12}} = \dfrac{{{h^3}.6\sqrt 6 .\sqrt 2 }}{{8.12}} = \dfrac{{{h^3}\sqrt 3 }}{8}\)
Tổng thể tích của ba khối tứ diện đều bị cắt đi là: \({V_0} = 3.\dfrac{{{x^3}\sqrt 3 }}{8}\)
Vì thể tích phần còn lại bằng một nửa thể tích khối tứ diện đều ban đầu nên, ta có: \(\dfrac{{3{x^3}\sqrt 3 }}{8} = \dfrac{1}{2}.\dfrac{{{h^3}\sqrt 3 }}{8} \Leftrightarrow 6{x^3} = {h^3} \Leftrightarrow x = \dfrac{h}{{\sqrt[3]{6}}}\)
Chọn D.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
