Cho khai triển (2 –<
Câu hỏi
Nhận biếtCho khai triển (2 –![\sqrt[3]{3}](http://images.tuyensinh247.com/picture/learning/exam/2013/1115/2782_23152_1.gif)
x)2n = a0 + a1x + ….+ a2nx2n.Tính hệ số a9, biết rằng số tự nhiên n thỏa mãn hệ thức 
+ 
+ 
+...+ 
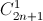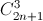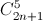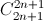= 4096 ( 
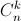là số tổ hợp chập k của n phần tử ).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Theo khai triển nhị thức Niutơn ta có 22n + 1 = (1+1)2n + 1
= 
+ 
+ 
+ 
+ ... + 
,
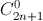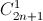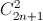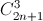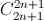02n +1 = ( 1 -1)2n + 1
= - + - +...-
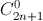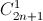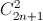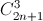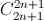
Suy ra 22n + 1 = 2( + + ... + )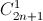
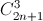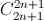Do đó (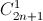 + + 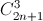... + 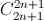) =22n.
Theo bài ra ta có 22n = 4096 = 212. Suy ra n = 6.
Khai triển (2 –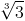 
x)12 = a0 + a1x + …+ a12x12 có số hạng a9x9 chính là 
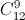212-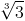9 (-)9x9.
Do đó a9 = 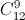212-9(-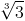)9 = -8.27. 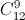= -47520.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
