Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=a và AA'= căn 2a. Góc giữa hai đường thẳng AB' và B
Câu hỏi
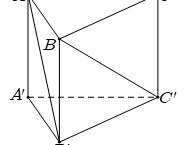
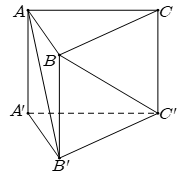
Nhận biếtCho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có \(AB=a\) và \(A{A}'=\sqrt{2}a.\) Góc giữa hai đường thẳng \(A{B}'\) và \(B{C}'\) bằng
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có \(\left\{ \begin{align} & \overrightarrow{A{B}'}=\overrightarrow{AB}+\overrightarrow{B{B}'} \\ & \overrightarrow{B{C}'}=\overrightarrow{BC}+\overrightarrow{C{C}'}=\overrightarrow{BC}+\overrightarrow{B{B}'} \\ \end{align} \right.\Rightarrow \overrightarrow{A{B}'}.\overrightarrow{B{C}'}=AB.BC.\cos {{120}^{0}}+B{{{B}'}^{2}}=\frac{3}{2}{{a}^{2}}.\)
Suy ra \(\cos \left( A{B}';B{C}' \right)=\frac{\left| \overrightarrow{A{B}'}.\overrightarrow{B{C}'} \right|}{A{B}'.B{C}'}=\frac{\frac{3}{2}{{a}^{2}}}{\sqrt{A{{B}^{2}}+B{{{{B}'}}^{2}}}.\sqrt{B{{C}^{2}}+C{{{{C}'}}^{2}}}}=\frac{\frac{3}{2}{{a}^{2}}}{{{a}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}}=\frac{1}{2}.\)
Vậy góc giữa hai đường thẳng \(A{B}'\) và \(B{C}'\) bằng \({{60}^{0}}.\)
Chọn D
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
