Cho hình lăng trụ tam giác ABC.A'B'C' có AA' = 2a; AB = AC = a (a > 0)
Câu hỏi
Nhận biếtCho hình lăng trụ tam giác ABC.A'B'C' có AA' = 2a; AB = AC = a (a > 0) và góc giữa cạnh bên AA' và mặt phẳng (ABC) bằng 60o. Tính thể tích của khối lăng trụ ABC.A’B’C’ và khoảng cách từ điểm A đến mặt phẳng (A’BC) theo a biết rằng hình chiếu của điểm A’ trên mặt phẳng (ABC) trùng với trực tâm H của tam giác ABC.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Theo bài ra góc giữa cạnh bên AA' và mặt phẳng (ABC) bằng 60o nên góc A'AH = 60o và do AA'= 2a nên A'H= a√3 là một đường cao của khối lăng trụ ABC.A'B'C' và AH = a.
Mặt khác tam giác ABC cân tại A nên nếu gọi M là trung điểm của cạnh BC thì đoạn AM là 1 đường cao của tam giác ABC và AM < AC = AB = AH = a nên H nằm ngoài tam giác ABC và nằm trên tia đối của tia AM suy ra A là trọng tâm của tam giác HBC.
Khi đó ta có AM = 
=> BC= 2MC = a√3
=> SABC = 
.BC.AM =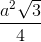 
Thể tích khối lăng trụ đã cho là: V = A'H SABC =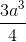 
Nối A'M ,ta có (A'HM) ⊥ BC khi đó kẻ HK ⊥ A'M, K ∈ A'M thì HK ⊥ (A'BC) nên d(H; (A'BC)) = HK. Ta có:
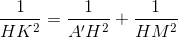=>....=> HK =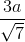 
Suy ra khoảng cách d(H, (A'BC)) =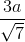
Ta lại có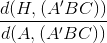 
= 
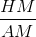= 3
Vậy khoảng cách d(A; (A'BC)) = 
.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
