Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước AB = a AD = b AA’ = c. Trong các kết quả sau đâ
Câu hỏi
Nhận biếtCho hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước AB = a, AD = b, AA’ = c. Trong các kết quả sau đây, kết quả nào là sai?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
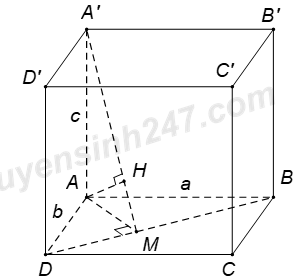
Xét các đáp án:
Đáp án A. Ta có
\(B{D}'=\sqrt{B{{D}^{2}}+DD{{'}^{2}}}=\sqrt{A{{B}^{2}}+A{{D}^{2}}+AA{{'}^{2}}}=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}.\)
Vậy A đúng.
Đáp án B. Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot CC'\end{array} \right. \Rightarrow \,d\left( {AB,CC'} \right) = BC = b.\)
Vậy B đúng.
Đáp án C. Ta có \(B{B}'\parallel D{D}'\Rightarrow d\left( B{B}',D{D}' \right)=BD=\sqrt{{{a}^{2}}+{{b}^{2}}}.\)
Vậy C đúng. Đáp án D. Gọi M là hình chiếu của A trên AB, H là hình chiếu của A trên AM. Ta có :
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AM\\BD \bot AA'\end{array} \right. \Rightarrow BD \bot \left( {A'AM} \right) \Rightarrow BD \bot AH\\\left\{ \begin{array}{l}AH \bot BD\\AH \bot A'M\end{array} \right. \Rightarrow AH \bot \left( {A'BD} \right) \Rightarrow d\left( {A;\left( {A'BD} \right)} \right) = AH\\\frac{1}{{A{H^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{A{{A'}^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{AA{'^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} \Rightarrow AH = \frac{1}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }}\end{array}\).
Vậy D sai.
Chọn D
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
