Cho hình chóp S.ABCD đáy là hình thang vuông tại A và B AB = BC = a;AD = 2a. Biết SA vuông góc với đ
Câu hỏi
Nhận biếtCho hình chóp S.ABCD đáy là hình thang vuông tại A và B, \(AB = BC = a;\,\,AD = 2a\). Biết SA vuông góc với đáy (ABCD), \(SA = a\). Gọi M, N lần lượt là trung điểm SB, CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
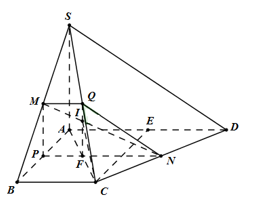
Gọi P và Q lần lượt là trung điểm của AB và SC ta có : MQ // NP // BC \( \Rightarrow M,N,P,Q\) đồng phẳng.
Gọi \(F = NP \cap AC \Rightarrow \left( {MNPQ} \right) \cap \left( {SAC} \right) = QF\),
\(I = QF \cap MN \Rightarrow I = MN \cap \left( {SAC} \right)\).
Gọi E là trung điểm của AD, ABCE là hình vuông nên CE = a.
Xét tam giác ACD có \(CE = \dfrac{1}{2}AD = a \Rightarrow \Delta ACD\) vuông tại C \( \Rightarrow CD \bot AC\).
Ta có:
\(\left\{ \begin{array}{l}CD \bot AC\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow NC \bot \left( {SAC} \right) \Rightarrow \)C là hình chiếu của N trên (SAC)
\( \Rightarrow \angle \left( {MN;\left( {SAC} \right)} \right) = \angle \left( {NI;CI} \right) = \angle NIC\).
Xét tam giác vuông CED có \(CD = \sqrt {C{E^2} + E{D^2}} = a\sqrt 2 \Rightarrow CN = \dfrac{{a\sqrt 2 }}{2}\).
Có \(MO = \dfrac{1}{2}BC = \dfrac{a}{2};\,\,NP = \dfrac{{AD + BC}}{2} = \dfrac{{3a}}{2}\); \(\dfrac{{PF}}{{BC}} = \dfrac{{AP}}{{AB}} = \dfrac{1}{2} \Rightarrow PF = \dfrac{a}{2} \Rightarrow FN = a\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{IN}}{{IM}} = \dfrac{{NF}}{{MQ}} = 2 \Rightarrow IN = 2IM \Rightarrow IN = \dfrac{2}{3}MN\).
Xét tam giác vuông MNP có \(MN = \sqrt {M{P^2} + N{P^2}} = \sqrt {{{\left( {\dfrac{{SA}}{2}} \right)}^2} + N{P^2}} = \dfrac{{a\sqrt {10} }}{2} \Rightarrow IN = \dfrac{2}{3}.\dfrac{{a\sqrt {10} }}{2} = \dfrac{{a\sqrt {10} }}{3}\).
Xét tam giác vuông NIC : \(\sin \angle NIC = \dfrac{{CN}}{{NI}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt {10} }}{3}}} = \dfrac{{3\sqrt 5 }}{{10}}\).
Chọn C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
