Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA = a và SA vuông góc với đáy. Tang của góc giữa đường thẳng SO và mặt phẳng (SAB) bằng
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
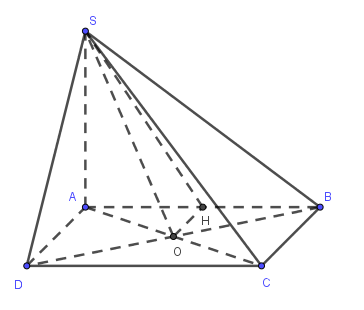
Gọi H là trung điểm của AB \(\Rightarrow OH//AD\)
ABCD là hình vuông \(\Rightarrow AD\bot AB\) \(\Rightarrow OH\bot AB\)
Mà \(OH\bot SA,\,\,(vi\,SA\bot (ABCD))\)
\(\Rightarrow OH\bot (SAB)\)
\(\Rightarrow SH\) là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
\(\Rightarrow \left( \widehat{SO,(SAB)} \right)=\left( \widehat{SO,SH} \right)=\widehat{HSO}\)
Ta có: OH là đường trung bình của tam giác ABD \(\Rightarrow OH=\frac{1}{2}AD=\frac{a}{2}\)
Tam giác SAH vuông tại A \(\Rightarrow SH=\sqrt{S{{A}^{2}}+A{{H}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{5}}{2}\)
Tam giác SHO vuông tại H: \(\tan \widehat{HSO}=\frac{OH}{SH}=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\)
\(\Rightarrow \tan \left( \widehat{SO,(SAB)} \right)=\frac{\sqrt{5}}{5}\).
Chọn: D
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
