Cho hình chóp S.ABCD có đáy ABCD là hình thoi hai đường chéo AC = 2√3a BD = 2a và cắt nhau tại O ha
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thoi, hai đường chéo AC = 2√3a , BD = 2a và cắt nhau tại O, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng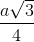 
, tính thể tích khối chóp S.ABCD theo a, và góc giữa 2 mặt phẳng (SAB) với (SBD).
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Từ giả thiết AC = 2a√3; BD = 2a và AC, BD vuông góc với nhau tại trung điểm O của mỗi đường chéo. Ta có ∆ABO vuông tại O và AO = a√3; BO = a. Gọi K là hình chiếu của O trên AB, gọi I là hình chiếu của O trên SK.
Từ giả thiết 2 mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD) nên giao tuyến của chúng là SO ⊥ (ABCD)
Ta chứng minh được khoảng cách O tới (SAB) là đoạn OI
Ta có trong tam giác vuông AOB ta có:
= 
+ 
= 
+ 
=> OK = 
Tam giác SOK vuông tại O, OI là đường cao
=> 
= + 
=> SO = 
.
Diện tích đáy SABCD = 4S∆ABO = 2.OA.OB = 2√3a2
Đường cao của hình chóp SO = 
Thể tích khối chóp S.ABCD: VS.ABCD = 
SABCD.SO = 
Ta có hình chiếu của tam giác SAB trên mặt phẳng (SBD) là ∆SBO
Gọi α là góc giữa 2 mặt phẳng (SAB) và (SBD) ta có cosα =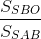 
Ta có SSBO = 
OB.SO = 
, SK = a => SSAB = a2
=> cosα = 
=> α = arccos
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.