Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a <
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,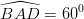 
, tam giác SBC cân tại S. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trên đường thẳng AC. Mặt phẳng (SCD) tạo với đáy (ABCD) góc 
.
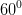1. Tính thể tích của khối chóp S.ABCD theo a
2. Tính khoảng cách giữa 2 đường thẳng AD và SC theo a
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
1. Gọi H là hình chiếu vuông góc của S trên (ABCD) thì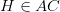 
(1)
ABCD là hình thoi => HB = HD => SB = SD = SC
Gọi M là trung điểm DC => SM ⊥ DC (2)
Từ (1) và (2) DC ⊥ (SHM) =>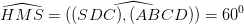 
Ta có: BD = a; AC =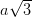 
, BO = DO = 
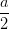; AO = CO =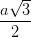 
Hai tam giác CMH và COD đồng dạng
=> 
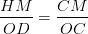=> HM = 
= 
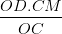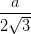
Lại có: h = SH = MH. tan 60 = a/2
=> 
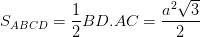
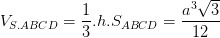
Vậy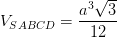 
2. Vì AD // (SBC) => d (AD,SC) = d (AD,(SBC)) = d(D,(SBC))
Có SM =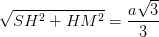 
d(D,(SBC)) =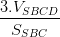 
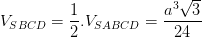
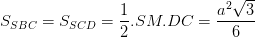
=> d (AD,SC)= d(D,(SBC)) = =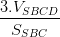 
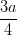
Vậy d (AD,SC)=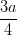
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
