Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a AD = 2a cạnh SA vuông góc với đáy cạnh SB t
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2a, cạnh SA vuông góc với đáy, cạnh SB tạo với mặt phẳng đáy một góc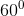 
. Trên cạnh SA lấy điểm M sao cho AM = 
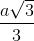. Mặt phẳng BCM cắt cạnh SD tại N. Tính thể tích khối chóp S.BCNM.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Tính thể tích của hình chóp S.BCNM
Mặt phẳng (BCM) // AD nên nó cắt mặt phẳng (SAD) theo giao tuyến MN//AD
Ta có: BC ⊥ AB và BC⊥ SA => BC ⊥BM
Tứ giác BCNM là hình thang vuông BM là đường cao.
Ta có: SA =AB. tan 60 = 
<=> 
=> MN = 
BM = 
Diện tích hình thang BCNM là : S = 
Hạ SH ⊥ BM
Ta có: SH ⊥BM
Và BC ⊥ (SAB) 
(SBM)=> BC ⊥ SH. Vậy SH ⊥ (BMNC)
=> SH là đường cao của khối chóp S.BCNM
Trong tam giác SBA ta có: SB = 
=> 
Vậy BM là phân giác của góc 
Vậy thể tích khối chóp S.BCNM là
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.