Cho hình chóp đều S.ABCD có AB = a√2, góc giữa SA và (ABCD) bằng 600.
Câu hỏi
Nhận biếtCho hình chóp đều S.ABCD có AB = a√2, góc giữa SA và (ABCD) bằng 600. Gọi G là trọng tâm tam giác SBD, mặt phẳng (P) qua G và song song với mặt phẳng (ABCD) lần lượt cắt SA, SB, SC, SD tại các điểm A’, B’, C’, D’. Tính thể tích khối đa diện ABCDA’B’C’D’ và bán kính mặt cầu ngoại tiếp hình chóp S.ABD.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi H = BD ∩ AC, AB = a√2 => BD = a√2.√2 = 2a
G là trọng tân tam giác.
Vì (P) // (ABCD) => B'D' // BD
Và A'B'C'D' là hình vuông => 
= 
= 
=> B'D' = BD = 
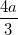
=> A'B' = A'D' = 
= 
a. (do A'B'C'D' là hình vuông nên tam giác A'B'D' vuông cân tại A')
Vì S.ABCD là hình chóp đều nên SH ⊥ (ABCD)
=> góc giữa SA và (ABCD) là 
= 60o
Trong tam giác vuông ABD có AH = 
BD = a
Xét tam giác SAH vuông tại H: SH = HA. tan600 = a√3 => SA = 2a
Ta có VS.ABCD = 
. SH. SABCD = . a√3. a√2. a√2 =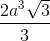 
Ta có SG = 
SH =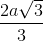 
VS.A'B'C'D' = . SG. SA'B'C'D' = . 
. a. a =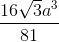 
VABCD.A'B'C'D' = VS.ABCD - VS.A'B'C'D' = - =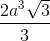 
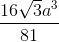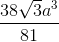
Gọi O, R lần lượt là tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABD
Suy ra O ∈ SH => O ∈ (SBD) suy ra R là bán kính đường tròn ngoại tiếp tam giác SBD mà SB = SD = BD = 2a
Suy ra tam giác SBD đều nên R = 
=
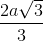
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
