Cho hàm số y=x3+2(m-1)x2+(m2-4m+1)x-2(m2+1) (1) 1.khảo sát sự biến th
Câu hỏi
Nhận biếtCho hàm số y=x3+2(m-1)x2+(m2-4m+1)x-2(m2+1) (1) 1.khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m=0 (học sinh tự giải) 2.Tìm các giá trị của m để hàm số có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số (1) vuông góc với đường thẳng y=x+5
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
1.Học sinh tự giải
2.Ta có y’=3x2+4(m-1)x+m2-4m+1
Hàm số có CĐ, CT <=> y’=0 có hai nghiệm phân biệt x1, x2 và y’ đổi dấu khi x đi qua mỗi nghiệm này
<=> ∆’=m2+4m+1>0 <=> m>-2+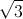
hoặc m< -2- (*)
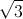Nhận xét: hai đường thẳng vuông góc với nhau thì tích hệ số góc của chúng bằng (-1). Ta sẽ xác định hệ số góc của đường thẳng đi qua CĐ CT của hàm số bằng(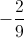
)
Gọi A(x1;y1), B(x2;y2) là các điểm cực trị của đồ thị hàm số và k là hệ số góc của đưởng thẳng AB. Khi đó:
k=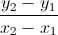
=
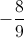(m-1)2+
(m2-4m+1)
Suy ra: 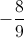(m-1)2+(m2-4m+1)=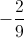 <=> m2+4m=0 <=>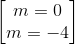 
Cả hai giá tri này của m đều thỏa mãn điều kiện (*)
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.