Cho hàm số y = x3 - 3x2 + 4 , (C) Khảo sát sự biến thiên và vẽ đồ thị
Câu hỏi
Nhận biếtCho hàm số y = x3 - 3x2 + 4 , (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (HS tự làm)
Tìm k để đường thẳng d : y = kx + k cắt đồ thị (C) tại 3 điểm phân biệt
A(-1;0) , M, N và MN ≤ 2√2
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
* TXĐ : R
* 
= +∞; 
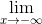y = -∞
* y' = 3x2 – 6x
y' = 0 ⇔ x = 0, x = 2
* Bảng BT :
*Trả lời : hàm số đồng biến trên các khoảng (-∞; 0) và (2;+∞)
hs nghịch biến trên (0;2)
Điểm cực đại (0;4)
Điểm cực tiểu (2,0)
* Vẽ đồ thị (HS tự vẽ)
*Phương trình hoành độ giao điểm : x3– 3x + 4 = k(x + 1)
⇔ (x2 – 4x + 4 – k)(x + 1) = 0
⇔ x = -1; g(x) = x2 – 4x + 4 – k = 0
Đường thẳng (d) cắt (C) tại ba điểm phân biệt A(-1;0);M, N khi g(x) = 0 có hai nghiệm phân biệt x1, x2 ≠ -1
⇔ ∆’ = k > 0 và g(-1) = 9 – k ≠ 0 ⇔ 0 < k ≠ 9
gọi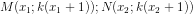 
*MN2 = (x2 – x1)2 + [kx2 + k – kx1 – k]2
(x2 – x1)2 + k2(x2 – x1)2
= (k2 + 1)[(x1 + x2)2 – 4x1x2]
MN ≤ 2√2 ⇔ (k2 + 1)[16 – 4(4 – k)] ≤ 8
⇔ k3 + k – 2 ≤ 0
⇔ (k – 1)(k2 + k + 2) ≤ 0
⇔ k ≤ 1
Đối chiếu với điều kiện : 0 < k ≤ 1
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.