Cho hàm số y = x3 - 3x + 1, có đồ thị (C) Khảo sát sự biến thiên và
Câu hỏi
Nhận biếtCho hàm số y = x3 - 3x + 1, có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) (HS tự làm)
Tìm tọa độ điểm A thuộc đồ thị (C), biết rằng tiếp tuyến của đồ thị (C) tại điểm A cắt đồ thị tại B (khác điểm A) thỏa mãn xA + xB = 1 (trong đó xA, xB lần lượt là hoành độ các điểm A và B)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
+ Tập xác định: R
+ Sự biến thiên :
- Chiều biến thiên : y' = 3x2 - 3; y' = 0 ⇔ x = 1; x = -1
Hàm số đồng biến trên các khoảng (-∞;-1) và (1;+∞) . Hàm số nghịch biến trên khoảng (-1;1)
- Cực trị : Hàm số đạt cực đại tại x = -1 và Ycđ = 3. Hàm số đạt cực tiểu tại x = 1;
Yct = -1
- Giới hạn : 
y = -∞; 
y = +∞
- Bảng biến thiên
+ Đồ thị
Gọi điểm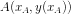 
Phương trình tiếp tuyến tại điểm A có dạng :
: y = y’(xA)(x – xA) + y(xA) hay y = (3xA2 – 3)x – 2xA3 + 1 (∆)
Hoành độ giao điểm của tiếp tuyến ∆ với đồ thị (C) là nghiệm của phương trình : x3 –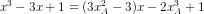 
Từ giả thiết : xA + xB = 1 => xB = 1 – xA và hoành độ giao điểm của B thỏa mãn phương trình (1) nên :
(1 – xA)3 – 3xA2(1 – xA) + 2xA3 = 0 ⇔ 4xA3 – 3xA + 1 = 0 ⇔ xA = -1
hoặc xA = 
Với xA = -1 => A(-1;3)
Với xA = => xB = nên A ≡ B (loại)
Vậy A(-1;3) là điểm cần tìm
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.