Cho hàm số <
Câu hỏi
Nhận biếtCho hàm số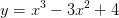 
có đồ thị là (C). Gọi 
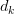là đường thẳng đi qua điểm A( -1; 0 ) với hệ số góc k. Tìm k để đường thẳng 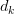cắt đồ thị (C) tại ba điểm phân biệt A, B, C và giao điểm B, C cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 1.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Phương trình đường thẳng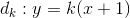 
( 0,25đ)
Phương trình hoành độ giao điểm:
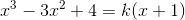(1)
<=> 
<=> 
<=> 
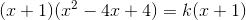
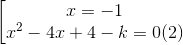(0,5đ)
Đường thẳng cắt đồ thị tại 3 điểm A, B, C
<=> PT (1) có 3 nghiệm phân biệt
<=> PT (2) có 2 nghiệm phân biệt khác -1
<=> 
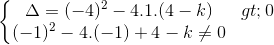(0,5đ)
<=> 
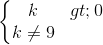( 0,25đ)
Gọi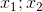 
là 2 nghiệm của phương trình (2). Theo Viet ta có 
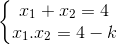( 0,25đ)
Do A(-1;0) => 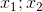là hoành độ của B và C
=> 
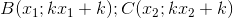( 0,25đ)
Có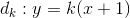
<=> 
=> 
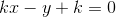
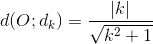( 0,25đ)
=> 
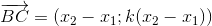
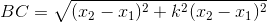
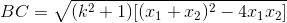
Theo Viet ta có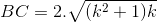 
( 0,25đ)
=> 
<=> 
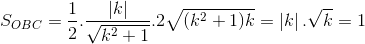
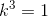=> k =1 ( thỏa mãn ) ( 0,5đ)
Vậy k=1 thỏa mãn yêu cầu của bài toán
( Chú y : gt nghĩa là dấu > ; lt nghĩa là dấu < )
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.