Cho các số thực dương x, y thỏa mãn: X2 – xy + 3
Câu hỏi
Nhận biếtCho các số thực dương x, y thỏa mãn:
X2 – xy + 3 = 0 và 2x + 3y ≤ 14
Tìm GTLN, GTNN của biểu thức P = 3x2y - xy2 – 2x(x2 – 1)
Đáp án đúng: B
Lời giải của Tự Học 365
Lời giải chi tiết:
Ta có: x2 – xy + 3 = 0
<=> xy = x2 + 3
<=> y =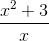 
Mà 2x + 3y ≤ 14
<=> 2x + 3 .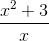 ≤ 14
<=> 2x2 + 3x2 +9 ≤ 14x
<=> 5x2 – 14x + 9 ≤ 0
<=> x ∈ [1, 9/5]
=> P =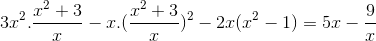 
= f(x)
Có f '(x) = 5 +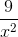 
> 0 ∀ x ∈ [1; 9/5]
Bảng biến thiên:
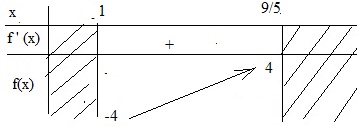
=> Min f(x) = -4 khi x = 1
x ∈ [1; 9/5]
Max f(x) = 4 khi x = 9/5
x ∈ [1; 9/5]
=> Min P = -4 khi x = 1, y = 4
Max P = 4 khi x = 9/5; y = 52/15
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.