Cho a, b là các số dương thỏa mãn: ab + a + b = 3. Chứng minh:
Câu hỏi
Nhận biếtCho a, b là các số dương thỏa mãn: ab + a + b = 3.
Chứng minh: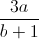 
+ 
+ 
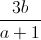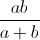≤ a2 + b2 + .
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Từ giả thiết a, b > 0 và ab + a + b = 3
=> ab = 3 - (a + b), (a + 1)(b + 1) = ab + a +b +1 = 4.
Bất đẳng thức đã cho tương đương với
a2 + b2 + 
≥ 
+ 
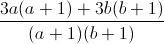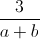- 1
⇔ a2 + b2 + ≥ 
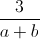(a2 + b2 )+ ( a + b ) + - 1
⇔ 4( a2 + b2 ) + 6 ≥ 3( a2 + b2 ) + 3( a + b ) +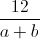 
- 4
⇔ a2 + b2 - 3( a + b ) - 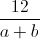+ 10 ≥ 0 (A)
Đặt x = a + b > 0 => x2 = ( a + b )2 ≥ 4ab = 4( 3 - x )
=> x2 + 4x - 12 ≥ 0 => x ≤ - 6 hay x ≥ 2 => x ≥ 2 ( vì x > 0 )
x2 = a2 + b2 + 2ab => a2 + b2 = x2 – 2( 3 – x ) = x2 + 2x - 6
Thế x như trên (A) ta thành
x2 – x -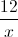 
+ 4 ≥ 0, với x ≥ 2
⇔ x3 – x2 + 4x – 12 ≥ 0, với x ≥ 2
⇔ ( x – 2 )( x2 + x + 6 ) ≥ 0, với x ≥ 2 (hiển nhiên đúng)
Vậy bất đẳng thức đã cho đã được chứng minh
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
