Câu hỏi và cách giải chi tiết
Câu hỏi
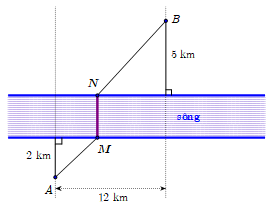
Nhận biết
Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố B cách bờ sông 5 (km ), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn\(AM\) là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
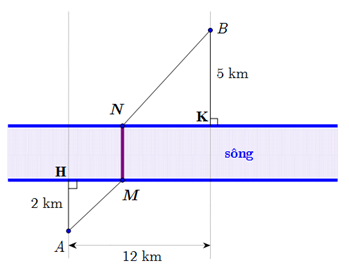
Dựng AH, BK như hình vẽ.
Gọi độ dài đoạn HM là x (km, 0 < x < 12)
Khi đó, NK = 12 – x
Khi đó ta có: \(AM = \sqrt {A{H^2} + H{M^2}} = \sqrt {{2^2} + {x^2}} \); \(NB = \sqrt {N{K^2} + B{K^2}} = \sqrt {{5^2} + {{\left( {12 - x} \right)}^2}} \).
Do MN không đổi, nên để tiết kiệm chi phí đi từ A đến B (tức là, độ dài đường gấp khúc AMNB ngắn nhất) thì \(AM + NB\) phải nhỏ nhất
Ta có: \(AM + NB = \sqrt {{2^2} + {x^2}} + \sqrt {{5^2} + {{\left( {12 - x} \right)}^2}} \ge \sqrt {{{\left( {2 + 5} \right)}^2} + {{\left( {x + 12 - x} \right)}^2}} = \sqrt {49 + 144} = \sqrt {193} \)
Khi đó, \({\left( {AM + NB} \right)_{\min }} = \sqrt {193} \) khi và chỉ khi \(\frac{x}{2} = \frac{{12 - x}}{5} = \frac{{x + 12 - x}}{{2 + 5}} = \frac{{12}}{7} \Rightarrow x = \frac{{24}}{7}\)
\( \Rightarrow AM = \sqrt {{2^2} + {{\left( {\frac{{24}}{7}} \right)}^2}} = \frac{{2\sqrt {193} }}{7}\;\left( {{\rm{km}}} \right){\rm{.}}\)
Chọn: A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.