Câu hỏi và cách giải chi tiết
Câu hỏi
Nhận biết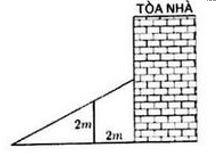
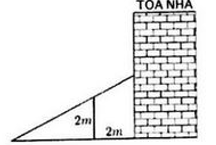
Một bức tường cao 2m nằm song song với tòa nhà và cách tòa nhà 2m. Người ta muốn chế tạo một chiếc thang bắc từ mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà (xem hình vẽ). Hỏi chiều dài tối thiểu của thang bằng bao nhiêu mét?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
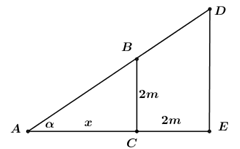
Gọi khoảng cách từ điểm đặt thang đến chân tường là \(x\ \left( x>0 \right)\) như trong hình vẽ.
Chiều dài cái thang là AD.
Gọi góc tạo bởi cái thang và mặt đất là \(\alpha .\)
Khi đó ta có: \(\tan \alpha =\frac{BC}{AC}=\frac{DE}{AE}\Rightarrow \frac{2}{x}=\frac{DE}{x+2}\) \(\Rightarrow DE=\frac{2\left( x+2 \right)}{x}.\)
Áp dụng định lý Pi-ta-go cho tam giác ADE vuông tại E ta được:
\(\begin{align} & A{{D}^{2}}=A{{E}^{2}}+D{{E}^{2}}={{\left( x+2 \right)}^{2}}+{{\left( \frac{2\left( x+2 \right)}{x} \right)}^{2}} \\ & \ \ \ \ \ \ \ =\frac{{{x}^{2}}{{\left( x+2 \right)}^{2}}+4{{\left( x+2 \right)}^{2}}}{{{x}^{2}}} \\ & \ \ \ \ \ \ \ =\frac{{{x}^{4}}+4{{x}^{3}}+8{{x}^{2}}+16x+16}{{{x}^{2}}}. \\ \end{align}\)
Đặt \(f\left( x \right)=\frac{{{x}^{4}}+4{{x}^{3}}+8{{x}^{2}}+16x+16}{{{x}^{2}}}.\)
Chiều cái thang ngắn nhất \(\Rightarrow A{{D}^{2}}\) đạt giá trị nhỏ nhất \(\Rightarrow \) hàm số \(y=f\left( x \right)\) đạt giá trị nhỏ nhất.
Ta có: \(f'\left( x \right)=\frac{2{{x}^{5}}+4{{x}^{4}}-16{{x}^{2}}-32x}{{{x}^{4}}}=\frac{2{{x}^{4}}+4{{x}^{3}}-16x-32}{{{x}^{3}}}.\)
\(\begin{array}{l}
\Rightarrow f'\left( x \right) = 0 \Leftrightarrow 2{x^4} + 4{x^3} - 16x - 32 = 0\\
\Leftrightarrow \left( {x - 2} \right)\left( {2{x^3} + 8{x^2} + 16x + 16} \right) = 0\\
\Leftrightarrow \left( {x - 2} \right)\left( {x + 2} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\;\;\left( {tm} \right)\\
x = - 2\;\;\left( {ktm} \right)
\end{array} \right.
\end{array}\)
Vậy với \(x=2\) thì chiều dài cái thang ngắn nhất: \(A{{D}^{2}}=f\left( x \right)=32\Rightarrow AD=\sqrt{32}=4\sqrt{2}m.\)
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.