Cần phải làm cái cửa sổ mà phía trên là hinh bán nguyệt phía dưới là hình chữ nhật có chu vi là a (m
Câu hỏi
Nhận biếtCần phải làm cái cửa sổ mà phía trên là hinh bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a (mét) (a chính là chi vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi đường kính của hình bán nguyệt). Hãy xác định d để diện tích cửa sổ là lớn nhất.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
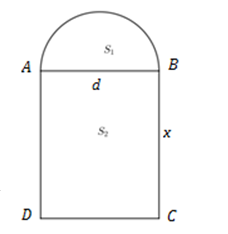
Đặt \(BC=x\) \(\left( x>0 \right)\). Chu vi cửa sổ là \(a=\pi \frac{d}{2}+2x+d\Rightarrow x=\frac{a}{2}-\frac{d}{2}\left( \frac{\pi }{2}+1 \right)\).
Diện tích cửa sổ là
\(f\left( d \right)=d.x+\frac{1}{2}\pi .\frac{{{d}^{2}}}{4}=\frac{ad}{2}-\frac{{{d}^{2}}}{2}\left( \frac{\pi }{2}+1 \right)+\pi .\frac{{{d}^{2}}}{8}=\frac{ad}{2}-\frac{{{d}^{2}}\left( \pi +4 \right)}{8}\).
Vì \(f\left( d \right)\) có đồ thị là một Parabol với bề lõm quay xuống và có hoành độ đỉnh là \(d=-\frac{\frac{a}{2}}{-\frac{\pi +4}{4}}=\frac{2a}{\pi +4}\).
Do đó diện tích cửa sổ lớn nhất khi \(d=\frac{2a}{\pi +4}\).
Chọn D
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.