Bảng biến thiên sau đây là của hàm số nào? <
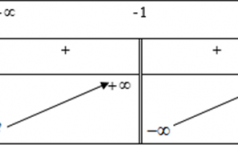
Câu hỏi
Nhận biếtBảng biến thiên sau đây là của hàm số nào?
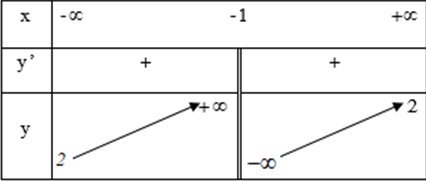
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Phương pháp:
- Quan sát bảng biến thiên.
- Khảo sát các hàm số của từng đáp án A, B, C, D.
Cách giải:
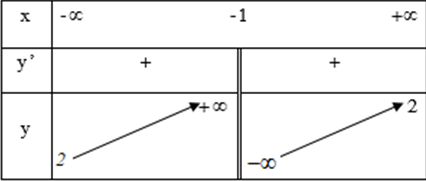
- Quan sát bảng biến thiên ta thấy:
+) \(\underset{x\to \pm \infty }{\mathop{\lim }}\,y=2\) nên đồ thị hàm số có tiệm cận đứng \(x=-1\).
+) \(\underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,y=+\infty ;\underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,y=-\infty \) nên đồ thị hàm số có tiệm cận ngang \(y=2\)
+ Hàm số đồng biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( -1;+\infty \right)\).
Đáp án A: Đồ thị hàm số \(y=\frac{x+1}{2x-1}\) có tiệm cận đứng \(x=\frac{1}{2}\Rightarrow \) loại.
Đáp án B: Đồ thị hàm số \(y=\frac{2x-1}{x+1}\) có tiệm cận ngang \(y=2\) và tiệm cận đứng \(x=-1\).Lại có \(y'=\frac{2\left( x+1 \right)-2x+1}{{{\left( x+1 \right)}^{2}}}=\frac{3}{{{\left( x+1 \right)}^{2}}}>0,\forall x\ne -1\) nên hàm số đồng biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( -1;+\infty \right)\Rightarrow \)thỏa mãn.
Đáp án C: \(y'=\frac{2\left( x+1 \right)-2x-3}{{{\left( x+1 \right)}^{2}}}=\frac{-1}{{{\left( x+1 \right)}^{2}}}<0,\forall x\ne -1\) nên hàm số nghịch biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( -1;+\infty \right)\Rightarrow \)loại.
Đáp án D: Đồ thị hàm số \(y=\frac{2x-1}{x-1}\) có tiệm cận đứng \(x=1\Rightarrow \) loại.Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.