Bạn Hoa đi từ nhà ở vị trí A đến trường học ở vị trí C phải đi qua cầu từ A đến B rồi từ B tới trườn
Câu hỏi
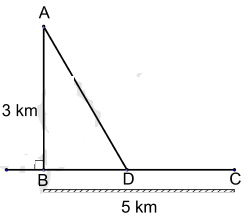
Nhận biếtBạn Hoa đi từ nhà ở vị trí A đến trường học ở vị trí C phải đi qua cầu từ A đến B rồi từ B tới trường. Trận lũ lụt vừa qua làm cây cầu bị ngập nước, dó đó bạn Hoa phải đi bằng thuyền từ nhà đến một vị trí D nào đó ở trên đoạn BC với vận tốc 4km/h sau đó đi với vận tốc 5km/h đến C. Biết độ dài AB = 3km, BC = 5km. Hỏi muộn nhất mấy giờ bạn Hoa phải xuất phát từ nhà để có mặt ở trường luc 7h30 phút sáng kịp vào học ?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Đặt BD = x (km) (0 ≤ x ≤ 5), thời gian Hoa đi quãng đường AD và DC lần lượt là \({{t}_{A\text{D}}}=\frac{\sqrt{{{x}^{2}}+{{3}^{2}}}}{4};{{t}_{DC}}=\frac{5-x}{5}\)
Thời gian đi học của Hoa là \(t={{t}_{AD}}+{{t}_{DC}}=\frac{\sqrt{{{x}^{2}}+9}}{4}+\frac{5-x}{5}\)
Xét hàm số \(f\left( x \right)=\frac{\sqrt{{{x}^{2}}+9}}{4}+\frac{5-x}{5}\) trên [0;5], có
\(f'\left( x \right)=\frac{x}{4\sqrt{{{x}^{2}}+9}}-\frac{1}{5}=0\Leftrightarrow 4\sqrt{{{x}^{2}}+9}=5x\Leftrightarrow 16\left( {{x}^{2}}+9 \right)=25{{x}^{2}}\Leftrightarrow {{x}^{2}}=16\Leftrightarrow x=4\)
Chứng minh được \(\min f\left( x \right)=f\left( 4 \right)=1,45\left( h \right)\) = 1 giờ 27 phút
Do đó để có mặt lúc 7h30 thì muộn nhất 6h03 phút Hoa phải xuất phát
Chọn đáp án B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.