Bạn An có một tâm bìa hình tròn như hình vẽ. An muốn biến hình tròn đó thành một cái phễu hình nón.
Câu hỏi
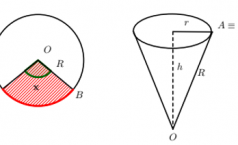
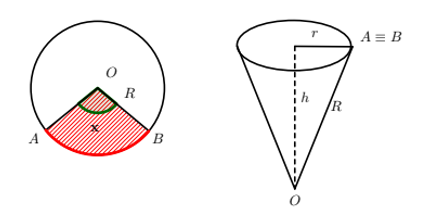
Nhận biếtBạn An có một tâm bìa hình tròn như hình vẽ. An muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó An phải cắt bỏ hình quạt tròn OAB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là góc ở tâm hình quạt tròn dùng để làm phễu. Tìm x để thể tích phễu lớn nhất.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Độ dài cung AB là xR cũng chính là chu vi đáy của hình nón \(\Rightarrow r=\frac{xR}{2\pi }\)
\(\Rightarrow h=\sqrt{{{R}^{2}}-\frac{{{x}^{2}}{{R}^{2}}}{4{{\pi }^{2}}}}=\frac{R}{2\pi }\sqrt{4{{\pi }^{2}}-{{x}^{2}}}\)
\(\Rightarrow \) Thể tích của hình nón \(V=\frac{1}{3}\pi {{\left( \frac{xR}{2\pi } \right)}^{2}}.\frac{R}{2\pi }\sqrt{4{{\pi }^{2}}-{{x}^{2}}}=\frac{\pi }{3}.{{\left( \frac{R}{2\pi } \right)}^{3}}{{x}^{2}}\sqrt{4{{\pi }^{2}}-{{x}^{2}}}\)
Xét hàm số
\(f'\left( x \right) = 2x\sqrt {4{\pi ^2} - {x^2}} + {x^2}\frac{{ - x}}{{\sqrt {4{\pi ^2} - {x^2}} }} = \frac{{2x\left( {4{\pi ^2} - {x^2}} \right) - {x^3}}}{{\sqrt {4{\pi ^2} - {x^2}} }} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\2\left( {4{\pi ^2} - {x^2}} \right) = {x^2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{2\sqrt 6 }}{3}\pi \end{array} \right.\)
Lập BBT ta thấy \(f{{\left( x \right)}_{\max }}=f\left( \frac{2\sqrt{6}}{3}\pi \right)\).
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
