Cho hình trụ có hai đáy là hai hình tròn ( O ) và ( O' ) chiều cao 2R và bán kính đáy R. Một mặt phẳ

Câu hỏi
Nhận biếtCho hình trụ có hai đáy là hai hình tròn \(\left( O \right)\) và \(\left( {{O}'} \right)\), chiều cao \(2R\) và bán kính đáy \(R\). Một mặt phẳng \(\left( \alpha \right)\) đi qua trung điểm của \(O{O}'\) và tạo với \(O{O}'\) một góc \(30{}^\circ \). Hỏi \(\left( \alpha \right)\) cắt đường tròn đáy theo một dây cung có độ dài bằng bao nhiêu?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
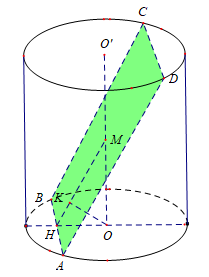
Gọi \(M\) là trung điểm của \(O{O}'\). Gọi \(A\), \(B\) là giao điểm của mặt phẳng \(\left( \alpha \right)\) và đường tròn \(\left( O \right)\) và \(H\) là hình chiếu của \(O\) trên \(AB\) \(\Rightarrow AB\bot \left( MHO \right)\).
Trong mặt phẳng \(\left( MHO \right)\) kẻ \(OK\bot MH\), \(\left( K\in MH \right)\) khi đó góc giữa \(O{O}'\) và mặt phẳng \(\left( \alpha \right)\) là góc \(\widehat{OMK}=30{}^\circ \). Xét tam giác vuông \(MHO\) ta có \(HO=OM\tan 30{}^\circ \)\(=R\tan 30{}^\circ \)\(=\frac{R\sqrt{3}}{3}\).
Xét tam giác vuông \(AHO\) ta có \(AH=\sqrt{O{{A}^{2}}-O{{H}^{2}}}\)\(=\sqrt{{{R}^{2}}-\frac{{{R}^{2}}}{3}}\)\(=\frac{R\sqrt{2}}{\sqrt{3}}\).
Do \(H\) là trung điểm của \(AB\) nên \(AB=\frac{2R\sqrt{2}}{\sqrt{3}}\).
Chọn A
Luyện tập
Câu hỏi liên quan
-










Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
 =
=  =
=  và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.

 là số thực và z2 =
là số thực và z2 =  là số ảo.
là số ảo.

