Cho hình lập phương ABCD.A'B'C'D' cạnh bằng 1. Gọi M là điểm trên mặt phẳng ( A'BD ) sao cho CM^2+B
Câu hỏi
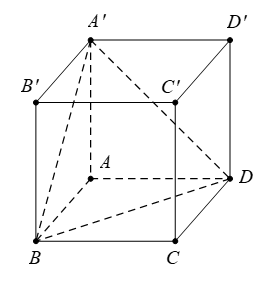
Nhận biếtCho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) cạnh bằng \(1.\) Gọi \(M\) là điểm trên mặt phẳng \(\left( {A}'BD \right)\) sao cho \(C{{M}^{2}}+{B}'{{M}^{2}}+{C}'{{M}^{2}}\) đạt giá trị nhỏ nhất. Tính \(MB.\)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gắn hệ trục tọa độ \(Oxyz,\) với \(A\left( 0;0;0 \right),\,\,B\left( 1;0;0 \right),\,\,D\left( 0;1;0 \right),\,\,{A}'\left( 0;0;1 \right).\)
Gọi \(G\) là trọng tâm của tam giác \({B}'{C}'C\)\(\Rightarrow \,\,\overrightarrow{G{B}'}+\overrightarrow{G{C}'}+\overrightarrow{GC}=\vec{0}.\)
Khi đó \(C{{M}^{2}}+{B}'{{M}^{2}}+{C}'{{M}^{2}}={{\left( \overrightarrow{MG}+\overrightarrow{GC} \right)}^{2}}+{{\left( \overrightarrow{MG}+\overrightarrow{G{B}'} \right)}^{2}}+{{\left( \overrightarrow{MG}+\overrightarrow{G{C}'} \right)}^{2}}\)
\(=3\,\,\times \,\,M{{G}^{2}}+2.\overrightarrow{MG}.\left( \overrightarrow{G{B}'}+\overrightarrow{G{C}'}+\overrightarrow{GC} \right)+G{{{B}'}^{2}}+G{{{C}'}^{2}}+G{{C}^{2}}\,\,\xrightarrow{{}}\,\,T.\)
Suy ra \({{T}_{\min }}\Leftrightarrow \,\,M{{G}_{\min }}\Leftrightarrow \) \(M\) là hình chiếu của \(G\) trên \(mp\,\,\left( {A}'BD \right).\)
Ta có \({B}'\left( 1;0;1 \right),\,\,{C}'\left( 1;1;1 \right)\Rightarrow \,\,G\left( 1;\frac{2}{3};\frac{2}{3} \right).\) Và \(\left[ \overrightarrow{{A}'B};\overrightarrow{{A}'D} \right]=\left( 1;1;1 \right).\)
Suy ra phương trình mặt phẳng \(\left( {A}'BD \right)\) là \(x+y+z-1=0\)\(\Rightarrow \,\,M\left( \frac{5}{9};\frac{2}{9};\frac{2}{9} \right).\) Vậy \(BM=\frac{2\sqrt{6}}{9}.\)
Chọn A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.