Một vật chuyển động theo quy luật s=-13t^3+6t^2 với t (giây) là khoảng thời gian tính từ khi vật bắt
Câu hỏi
Nhận biếtMột vật chuyển động theo quy luật \(s=-\frac{1}{3}{{t}^{3}}+6{{t}^{2}}\) với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi vật bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là bao nhiêu?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
\(v(t)=s'(t)=-{{t}^{2}}+12t\)
\(v'(t)=-2t+12t=0\Rightarrow t=6\)
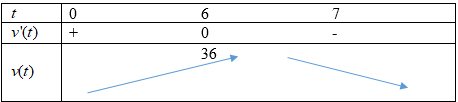
Vậy, vận tốc lớn nhất của vật đạt được là \(36(m/s)\).
Chọn: B
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.