Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 trung điểm A1B1C1D1 theo thứ tự của 4 c
Câu hỏi
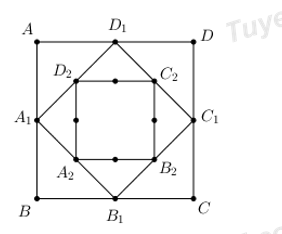
Nhận biếtCho hình vuông ABCD có cạnh bằng a và có diện tích \({{S}_{1}}\). Nối 4 trung điểm \({{A}_{1}},\,{{B}_{1}},\,{{C}_{1}},\,{{D}_{1}}\) theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích \({{S}_{2}}\). Tiếp tục làm như thế ta được hình vuông thứ ba\({{A}_{2}}{{B}_{2}}{{C}_{2}}{{D}_{2}}\) có diện tích \({{S}_{3}}\)…. Và cứ tiếp tục làm như thế ta được các hình vuông có diện tích \({{S}_{4}},\,{{S}_{5}},\,...,{{S}_{100}}\)(tham khảo hình vẽ bên). Tính tổng \(S={{S}_{1}}+{{S}_{2}}+{{S}_{3}}+...+{{S}_{100}}\).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Hình vuông ABCD cạnh a \(\Rightarrow {{S}_{1}}={{a}^{2}}\)
Hình vuông \({{A}_{1}}{{B}_{1}}{{C}_{1}}\,{{D}_{1}}\) có cạnh bằng \(\frac{a}{\sqrt{2}}\Rightarrow {{S}_{2}}=\frac{{{a}^{2}}}{2}\)
Hình vuông \({{A}_{2}}{{B}_{2}}{{C}_{2}}\,{{D}_{2}}\) có cạnh bằng \(\frac{\frac{a}{\sqrt{2}}}{\sqrt{2}}=\frac{a}{{{\left( \sqrt{2} \right)}^{2}}}\Rightarrow {{S}_{3}}=\frac{{{a}^{2}}}{{{2}^{2}}}\)
…
Hình vuông \({{A}_{99}}{{B}_{99}}{{C}_{99}}{{D}_{99}}\) có cạnh bằng \(\frac{a}{{{\left( \sqrt{2} \right)}^{99}}}\Rightarrow {{S}_{100}}=\frac{{{a}^{2}}}{{{2}^{99}}}\)
\(S={{S}_{1}}+{{S}_{2}}+{{S}_{3}}+...+{{S}_{100}}=\frac{{{a}^{2}}}{{{2}^{0}}}+\frac{{{a}^{2}}}{{{2}^{1}}}+\frac{{{a}^{2}}}{{{2}^{2}}}+...+\frac{{{a}^{2}}}{{{2}^{99}}}\,=\frac{{{a}^{2}}.\left( 1-{{\left( \frac{1}{2} \right)}^{100}} \right)}{1-\frac{1}{2}}=\frac{{{a}^{2}}\left( {{2}^{100}}-1 \right)}{{{2}^{100}}}.2=\frac{{{a}^{2}}\left( {{2}^{100}}-1 \right)}{{{2}^{99}}}\)
Chọn: B
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.