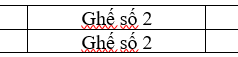
Cho hai dãy ghế được xếp như sau : <
Câu hỏi
Nhận biếtCho hai dãy ghế được xếp như sau :
Xếp 4 bạn nam và 4 bạn nữ vào hai dãy ghế trên. Hai người được gọi là ngồi đối diện với nhau nếu ngồi ở hai dãy và có cùng vị trí ghế (số ở ghế). Số cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ bằng
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Chọn 1 vị trí trong 2 vị trí đối xứng có \(C_{2}^{1}\) cách chọn, như vậy có \({{\left( C_{2}^{1} \right)}^{4}}={{2}^{4}}\) cách chọn ghế cho 4 bạn nam.
4 bạn nam này có thể đổi chỗ cho nhau nên có \(4!\) cách xếp.
Có \(4!\) cách xếp chỗ cho 4 bạn nữ còn lại.
Vậy có \(4!4!{{2}^{4}}\) cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ.
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.