Cho tứ diện ABCD có thể tích V. Gọi M N P Q lần lượt là trọng tâm tam giác ABC ACD ABD và BCD. Thể t
Câu hỏi
Nhận biếtCho tứ diện ABCD có thể tích \(V\). Gọi M, N, P, Q lần lượt là trọng tâm tam giác ABC, ACD, ABD và BCD. Thể tích khối tứ diện MNPQ bằng
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
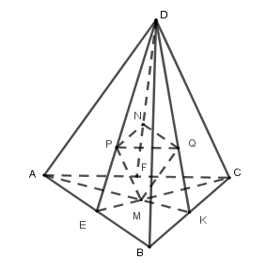
Gọi \(E,F,K\) là trung điểm của \(AB,AC,BC\).
Khi đó theo tính chất trọng tâm tam giác ta có \(\frac{DN}{DF}=\frac{DP}{DE}=\frac{DQ}{DK}=\frac{2}{3}\).
Suy ra \(\frac{{{V}_{DPNQ}}}{{{V}_{DEFK}}}=\frac{DN}{DF}.\frac{DP}{DE}.\frac{DQ}{DK}=\frac{2}{3}.\frac{2}{3}.\frac{2}{3}=\frac{8}{9}\).
Lại có \(\frac{{{V}_{M.NPQ}}}{{{V}_{D.NPQ}}}=\frac{\frac{1}{3}d\left( M;\left( NPQ \right) \right).{{S}_{NPQ}}}{\frac{1}{3}d\left( D;\left( NPQ \right) \right).{{S}_{NPQ}}}=\frac{1}{2}\) nên \({{V}_{MNPQ}}=\frac{4}{9}{{V}_{DEFK}}\).
Vì \(E;F;K\)là trung điểm của \(AB,AC,BC\) nên \({{S}_{EFK}}={{S}_{ABC}}-{{S}_{AEF}}-{{S}_{CFK}}-{{S}_{BEK}}=\frac{1}{4}{{S}_{ABC}}\).
Suy ra \(\frac{{{V}_{DEFK}}}{{{V}_{DABC}}}=\frac{\frac{1}{3}d\left( D;\left( EFK \right) \right).{{S}_{EFK}}}{\frac{1}{3}d\left( D;\left( ABC \right) \right).{{S}_{ABC}}}=\frac{1}{4}\)mà \({{V}_{MNPQ}}=\frac{4}{9}{{V}_{DEFK}}\)\(\Rightarrow {{V}_{MNPQ}}=\frac{1}{9}{{V}_{DABC}}=\frac{V}{9}\).
Chọn C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.