Trong không gian với hệ tọa độ Oxyz cho hai điểm A( 5; 0; 0 ) và B( 3; 4; 0 ). Với C là một điểm nằm
Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( 5;\ 0;\ 0 \right)\) và \(B\left( 3;\ 4;\ 0 \right)\). Với C là một điểm nằm trên trục Oz, gọi H là trực tâm tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính đường tròn đó bằng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
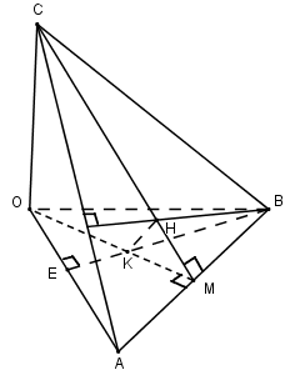
Dễ thấy \(\left( OAB \right)\equiv \left( Oxy \right),C\in Oz\Rightarrow OC\bot \left( OAB \right)\) \(B\left( 3;4;0 \right)\Rightarrow OB=\sqrt{{{3}^{2}}+{{4}^{2}}=5}=OA\Rightarrow \Delta OAB\) cân tại O.
Gọi H là trực tâm của tam giác ABC, gọi \(M=CH\cap AB\) ta có :
\(\left\{ \begin{align} & AB\bot CM \\ & AB\bot OC \\ \end{align} \right.\Rightarrow AB\bot \left( OCM \right)\Rightarrow AB\bot OM\), mà tam giác OAB cân tại O nên \(OM\bot AB\)
Gọi K là trực tâm của tam giác OAB ta có : \(\left\{ \begin{align} & BK\bot OA \\ & BK\bot OC \\ \end{align} \right.\Rightarrow BK\bot \left( OAC \right)\Rightarrow BK\bot AC\) \(\left\{ \begin{align} & AC\bot BK \\ & AC\bot BH \\ \end{align} \right.\Rightarrow AC\bot \left( BHK \right)\Rightarrow AC\bot HK\,\,\,\left( 1 \right)\)
\(AB\bot \left( OCM \right)\Rightarrow AB\bot HK\,\,\,\left( 2 \right)\)
Từ (1) và (2) \(\Rightarrow HK\bot \left( ABC \right)\Rightarrow HK\bot NM\Rightarrow \Delta HKM\) vuông tại H.
Ta có : M, K, (OCM) cố định, \(\widehat{KHM}={{90}^{0}}\) nên H thuộc đường tròn đường kính KM.
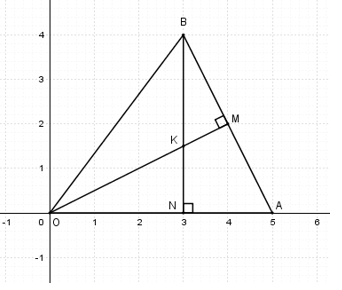
Dễ thấy
\(\begin{align} & \Delta BMK\backsim \Delta BNA\,\left( g.g \right)\Rightarrow \frac{MK}{NA}=\frac{BM}{BN} \\ & \Rightarrow \frac{MK}{2}=\frac{\frac{1}{2}AB}{4}\Leftrightarrow \frac{MK}{2}=\frac{\sqrt{5}}{4}\Leftrightarrow MK=\frac{\sqrt{5}}{2} \\ \end{align}\)
Vậy khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính đường tròn đó bằng \(\frac{MK}{2}=\frac{\sqrt{5}}{4}\)
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.