Cho hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều độ dài cạnh AB = 2a. Hình chiếu vuông gó
Câu hỏi
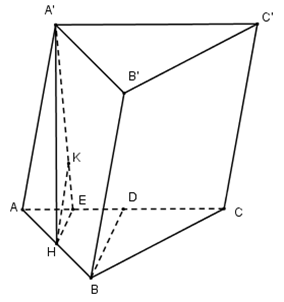
Nhận biếtCho hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A’ lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 600, tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC’A’).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Cách giải :
Ta có \(A'H\bot \left( ABC \right)\) nên \(\left( A'A;\left( ABC \right) \right)=\left( A'A;HA \right)=\widehat{A'AH}={{60}^{0}}\)
Gọi D là trung điểm của AC thì \(BD\bot AC\), kẻ HE // AC suy ra \(HE\bot AC\)
Ta có \(\left\{ \begin{align} & AH\bot AC \\ & HE\bot AC \\ \end{align} \right.\Rightarrow AC\bot \left( AHE \right)\)
Trong (AHE) kẻ \(HK\bot AE\Rightarrow HK\bot AC\Rightarrow HK\bot \left( ACC'A' \right)\Rightarrow d\left( H;\left( ACC'A' \right) \right)=HK\)
Mà \(\frac{d\left( B;\left( ACC'A' \right) \right)}{d\left( H;\left( ACC'A' \right) \right)}=\frac{BA}{BH}=2\Rightarrow d\left( B;\left( ACC'A' \right) \right)=2d\left( H;\left( ACC'A' \right) \right)=2HK\)
Ta có \(BD=\frac{2a\sqrt{3}}{2}=a\sqrt{3}\Rightarrow HE=\frac{1}{2}BD=\frac{a\sqrt{3}}{2}\)
Xét tam giác vuông A’AH có \(A'H=AH.\tan 60=a\sqrt{3}\)
Xét tam giác vuông A’HE có
\(\begin{align} & H{{K}^{2}}=\frac{A'{{H}^{2}}.H{{E}^{2}}}{A'{{H}^{2}}+H{{E}^{2}}}=\frac{3{{a}^{2}}.\frac{3{{a}^{2}}}{4}}{3{{a}^{2}}+\frac{3{{a}^{2}}}{4}}=\frac{3{{a}^{2}}}{5}\Rightarrow HK=\frac{a\sqrt{15}}{5} \\ & \Rightarrow d\left( B;\left( ACC'A' \right) \right)=\frac{2a\sqrt{15}}{5} \\ \end{align}\)
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
