Cho lăng trụ đứng ABC.A'B'C' có AB=AC=BB'=agóc BAC=120^circ . Gọi I là trung điểm của CC'. Tính cos
Câu hỏi
Nhận biếtCho lăng trụ đứng \(ABC.A'B'C'\) có \(AB=AC=BB'=a,\widehat{BAC}={{120}^{\circ }}\). Gọi I là trung điểm của \(CC'\). Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và \(\left( AB'I \right).\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
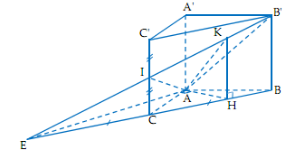
Gọi E là giao điểm của \(B'I\) và BC.
\(H\in BC\) sao cho \(EA\bot AH\) tại A
\(K\in B'I\) sao cho \(KH\bot CB\) tại H
Có \(KH\bot CB\Rightarrow KH\parallel CC'.\)
\(\Rightarrow KH\bot \left( ABC \right)\) tại H
\(\Rightarrow KH\bot EA\) mà \(EA\bot AH\)
\(\Rightarrow EA\bot \left( AKH \right)\)
\(\Rightarrow EA\bot AK\)
Hai mặt phẳng \(\left( AIB' \right)\) và \(\left( ACB \right)\) có giao tuyến là EA
Mà \(AK\subset \left( AIB' \right);AH\subset \left( ACB \right);EA\bot AK;EA\bot AH\Rightarrow \) góc hợp bởi hai mặt phẳng \(\left( AIB' \right)\) và \(\left( ACB \right)\) là \(\widehat{KAH}.\)
Ta có: \(BC=2a\cos {{30}^{\circ }}=a\sqrt{3}\)
\(A{{E}^{2}}=E{{C}^{2}}+A{{C}^{2}}-2AC.EC.\cos \widehat{ACE}\) \(=3{{a}^{2}}+{{a}^{2}}-2a.a\sqrt{3}.cos{{150}^{\circ }}=7{{a}^{2}}\)\(\Rightarrow AE=a\sqrt{7}\)
Ta cos: \(\cos \widehat{AEC}=\frac{A{{E}^{2}}+E{{C}^{2}}A{{C}^{2}}}{2.AE.EC}=\frac{7{{a}^{2}}3{{a}^{2}}-{{a}^{2}}}{2a\sqrt{7}.a\sqrt{3}}=\frac{9}{2\sqrt{21}}.\)
\(\Rightarrow \tan \widehat{AEC}=\sqrt{\frac{1}{{{\cos }^{2}}\widehat{AEC}}-1}=\frac{\sqrt{3}}{9}.\) \(\Rightarrow AH=AE.\tan \widehat{AEC}=\frac{a\sqrt{21}}{9}\)
Ta có: \(\frac{EH}{EB}=\frac{HK}{BB'}\) \(\Rightarrow HK=\frac{EH.BB'}{EB}=\frac{AE.BB'}{2BC.\cos \widehat{AEC}}=\frac{a\sqrt{7}.a.2\sqrt{21}}{2a\sqrt{3}.9}=\frac{7a}{9}.\)
\(\Rightarrow \cos\widehat{KAH}=\frac{AH}{AK}=\frac{AH}{\sqrt{A{{H}^{2}}+H{{K}^{2}}}}=\frac{a\sqrt{21}}{9\sqrt{\frac{21{{a}^{2}}}{81}+\frac{49{{a}^{2}}}{81}}}=\frac{\sqrt{30}}{10}.\)
Đáp án C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.