Cho khối chóp S.ABC có SA=SB=SC=a và góc ASB=góc BSC=góc CSA=30^0 . Mặt phẳng ( alpha ) qua A và cắ
Câu hỏi
Nhận biếtCho khối chóp S.ABC có \(SA=SB=SC=a\) và \(\widehat{ASB}=\widehat{BSC}=\widehat{CSA}={{30}^{0}}\) . Mặt phẳng \(\left( \alpha \right)\) qua A và cắt hai cạnh SB, SC tại B’, C’ sao cho chu vi tam giác AB’C’ nhỏ nhất. Tính \(k=\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}\)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
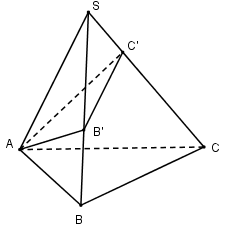
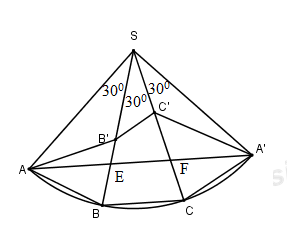
Trải các tam giác SAB, SBC, SAC ra cùng một mặt phẳng \(\left( A'\equiv A \right)\). Ta có \(\Delta SAC=\Delta SA'C\Rightarrow AC'=A'C'\)
Do đó chu vi tam giác AB’C’ là \(AB'+B'C'+C'A=AB'+B'C'+C'A\ge AA'\)
Dấu “=” xảy ra khi \(B'\equiv E,C'\equiv F\) hay \(SB'=SE,SC'=SF.\)
Tam giác SAA’ có góc S = 900, SA = SA’ = a nên tam giác SAA’ vuông cân tại S, do đó \(\widehat{SAA'}=\widehat{SA'A}={{45}^{0}}\).
Xét tam giác SAE có \(\widehat{SEA}={{180}^{0}}-{{30}^{0}}-{{45}^{0}}={{105}^{0}}\). Áp dụng định lí sin ta có:
\(\frac{SE}{\sin \widehat{SAE}}=\frac{SA}{\sin \widehat{SEA}}\Rightarrow \frac{SE}{\sin 45}=\frac{a}{\sin 105}\Rightarrow SE=\left( -1+\sqrt{3} \right)a\)
Hoàn toàn tương tự ta cũng chứng minh được \(SF=\left( -1+\sqrt{3} \right)a\)
Vậy chu vi tam giác AB’C” nhỏ nhất khi và chỉ khi \(SB'=SC'=\left( -1+\sqrt{3} \right)a\)
Khi đó \(\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}=\frac{SB'}{SB}.\frac{SC'}{SC}={{\left( -1+\sqrt{3} \right)}^{2}}=4-2\sqrt{3}\Rightarrow k=4-2\sqrt{3}\).
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.